题目内容
9.求证:任何两个连续正整数的乘积中没有完全平方数.分析 设两个正整数分别是n、n+1,得到n(n+1)的值介于两个连续正整数的平方之间,依此即可求解.
解答 证明:设两个正整数分别是n、n+1,则:
n2<n(n+1)=n2+n<n2+2n+1=(n+1)2,
则n(n+1)的值介于两个连续正整数的平方之间,
故任何两个连续正整数的乘积中没有完全平方数.
点评 考查了完全平方数,本题关键是理解完全平方数的定义,得到n(n+1)的值的范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.下列计算正确的是( )
| A. | $\sqrt{225}$=±15 | B. | $\sqrt{(-3)^{2}}$=-3 | C. | $\sqrt{(\frac{1}{36})^{2}}$=$\frac{1}{6}$ | D. | $\sqrt{\frac{36}{25}}$=$\frac{6}{5}$ |
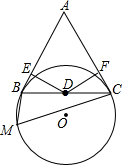 如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M为⊙O上一点,并且∠BMC=60°.
如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M为⊙O上一点,并且∠BMC=60°.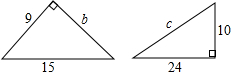 求图中直角三角形中未知的长度:b=12,c=26.
求图中直角三角形中未知的长度:b=12,c=26.