��Ŀ����
16��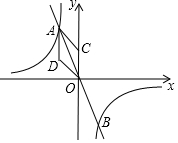 ��ͼ������������$y=\frac{k}{x}$��y=mx����A��B���㣬���A��B������ֱ�ΪA��x1��y1����B��x2��y2����S=|x1y1|����$\frac{3}{s-1}=\frac{4}{s}$��
��ͼ������������$y=\frac{k}{x}$��y=mx����A��B���㣬���A��B������ֱ�ΪA��x1��y1����B��x2��y2����S=|x1y1|����$\frac{3}{s-1}=\frac{4}{s}$����1����k��ֵ��
��2����m�仯ʱ������ʽ$\frac{��{m}^{2}-1��{x}_{1}{y}_{2}}{��m+1��^{2}}+\frac{2{x}_{2}{y}_{1}}{m+1}$�Ƿ�Ϊһ���̶���ֵ�����ǣ������ֵ�������ǣ���˵���ɣ�
��3����C��y���ϣ���D�������ǣ�-1��$\frac{3}{2}$������������ACOD��x�Ḻ����ƽ��m����λ����ƽ�ƹ����У���˫���������εı�ADʼ���н��㣬��ֱ��д��m��ȡֵ��Χ��
���� ��1��������֪�����õ�k��0������$\frac{3}{s-1}=\frac{4}{s}$�����ǵõ�s=4��k=-4��
��2�����ݷ�����������ͼ���ǹ���ԭ��O�����ĶԳ�ͼ�Σ�����OA=OB�����ǵõ�x1=-x2��y1=-y2��x1y2=x2y1���������ʽ���ɵõ����ۣ�
��3����ͼ������ƽ�Ƶ����ʵõ�D'��-1-m��$\frac{3}{2}$�����õ���D'��������Ϊ3�����뺯��y=-$\frac{4}{x}$��x��0�����ɵõ����ۣ�
��� �⣺��1������������$y=\frac{k}{x}$��ͼ���ڵڶ������ޣ�
��k��0��
��$\frac{3}{s-1}=\frac{4}{s}$��
��ã�s=4��
��k=-|x1y1|=-s=-4��
��2���߷�����������ͼ���ǹ���ԭ��O�����ĶԳ�ͼ�Σ�
��OA=OB��
��x1=-x2��y1=-y2��
��x1y2=x2y1��
$\frac{��{m}^{2}-1��{x}_{1}{y}_{2}}{��m+1��^{2}}+\frac{2{x}_{2}{y}_{1}}{m+1}$=$\frac{{x}_{1}{y}_{2}}{��m+1��^{2}}��{m}^{2}-1+2m+2��$=x2y1=x2•��-$\frac{4}{{x}_{1}}$��=4��
�����ʽ�Ƿ�Ϊһ���̶���ֵ4��
��3�� ��ͼ��
��ͼ��
������ACOD��x�Ḻ����ƽ��m����λ��
ʹ�õ�D�����ڷ���������y=-$\frac{4}{x}$��ͼ���D'����
����D'��x��Ĵ��ߣ�����ΪF��
��D�������ǣ�-1��$\frac{3}{2}$����
��D'��-1-m��$\frac{3}{2}$����
���D'��������Ϊ3��
��D'���ں���y=-$\frac{4}{x}$��x��0����ͼ���ϣ�
��$\frac{3}{2}$=-$\frac{4}{x}$��
��x=-$\frac{8}{3}$��
��-1-m=-$\frac{8}{3}$��
��m=$\frac{5}{3}$��
��m��ȡֵ��Χ��0��m��$\frac{5}{3}$��
���� �����Ƿ����������ۺ��⣬��Ҫ�����˴���ϵ������������ʽ�����ε����ʣ��Ȿ��Ĺؼ��������������������ʽ���ѵ�����ж�����ACOD�ı�ADʼ�պ�˫�����н���ķֽ�㣮

| A�� | $\sqrt{{5}^{2}}$=��5 | B�� | $\sqrt{{��-5��}^{2}}$=-5 | C�� | ${��2\sqrt{3}��}^{2}$=12 | D�� | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ |
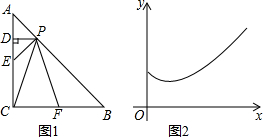 ��ͼ1����֪Rt��ABC��CA=CB����PΪAB���ϵ�һ�����㣬��E��F�ֱ���CA��CB�ߵ��е㣬����P��PD��CA��D����AP=x��ͼ��ij���߶εij�Ϊy�������ʾy��x�ĺ�����ϵ�Ĵ���ͼ����ͼ2��ʾ����ô�����߶ο����ǣ�������
��ͼ1����֪Rt��ABC��CA=CB����PΪAB���ϵ�һ�����㣬��E��F�ֱ���CA��CB�ߵ��е㣬����P��PD��CA��D����AP=x��ͼ��ij���߶εij�Ϊy�������ʾy��x�ĺ�����ϵ�Ĵ���ͼ����ͼ2��ʾ����ô�����߶ο����ǣ�������| A�� | PD | B�� | PE | C�� | PC | D�� | PF |
| A�� | $\frac{a}{b}$=$\frac{c}{d}$ | B�� | $\frac{a+1}{b+1}$=$\frac{c+1}{d+1}$ | C�� | $\frac{a+b}{b}$=$\frac{c+d}{d}$ | D�� | $\frac{a-c}{b-d}$=$\frac{a}{b}$ |
 ��ͼ��ʾAB�ǰ�Բ��ֱ����ͼ1�У���C�ڰ�Բ�⣻������̶ȵ�ֱ�߰�Ҫ��ͼ����ͼ�У�������ABC���������ߵĽ��㣮
��ͼ��ʾAB�ǰ�Բ��ֱ����ͼ1�У���C�ڰ�Բ�⣻������̶ȵ�ֱ�߰�Ҫ��ͼ����ͼ�У�������ABC���������ߵĽ��㣮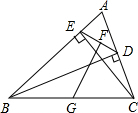 ��ͼ��BD��CE�ǡ�ABC��ͬ���ϵĸߣ���G��F�ֱ���BC��DE���е㣬��֤��GF��DE��
��ͼ��BD��CE�ǡ�ABC��ͬ���ϵĸߣ���G��F�ֱ���BC��DE���е㣬��֤��GF��DE��