题目内容
8.三角形的三边长是三个连续的自然数,且三角形的周长小于20,求三边的长.分析 利用三角形的三边长是三个连续的自然数,可设三角形三边的长分别为x-1,x,x+1,根据三角形三边的关系得到x-1+x>x+1,解得x>2,根据三角形的周长小于20得到x-1+x+x+1<20,解得x<$\frac{20}{3}$,从而得到x为3,4,5,6,然后分别计算出三角形三边的长.
解答 解:设三角形三边的长分别为x-1,x,x+1,则x-1+x>x+1,解得x>2,
∴x-1+x+x+1<20,解得x<$\frac{20}{3}$,
∴2<x<$\frac{20}{x}$且x为整数,
∴x为3,4,5,6,
当x=3时,三角形三边为2,3,4;
当x=4时,三角形三边为3,4,5;
当x=5时,三角形三边为4,5,6;
当x=6时,三角形三边为5,6,7.
点评 本题考查了三角形三边关系:三角形两边之和大于第三边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.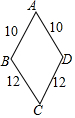 如图为两根长度均为10cm和两根长度均为12cm的木条组成的木框,为保证稳定要在BD间加一根木条.设该木条的长为xcm,则x的取值范围是( )
如图为两根长度均为10cm和两根长度均为12cm的木条组成的木框,为保证稳定要在BD间加一根木条.设该木条的长为xcm,则x的取值范围是( )
 如图为两根长度均为10cm和两根长度均为12cm的木条组成的木框,为保证稳定要在BD间加一根木条.设该木条的长为xcm,则x的取值范围是( )
如图为两根长度均为10cm和两根长度均为12cm的木条组成的木框,为保证稳定要在BD间加一根木条.设该木条的长为xcm,则x的取值范围是( )| A. | 0<x<20 | B. | 2<x<20 | C. | 0<x<24 | D. | 2<x<24 |
18.某中学七、八年级各选派10名选手参加学校举办的知识竞赛,竞赛计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下所示.
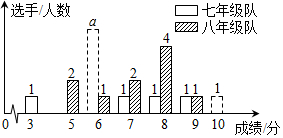
(1)请依据图表中的数据,求出a的值;并直接写出表格中m,p,q的值;
(2)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由、
| 队别 | 平均分 | 众数 | 中位数 | 方差 | 合格率 | 优秀率 |
| 七年级 | 6.7 | a | m | 3.41 | 90% | 20% |
| 八年级 | 7.1 | p | q | 1.69 | 80% | 10% |

(1)请依据图表中的数据,求出a的值;并直接写出表格中m,p,q的值;
(2)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由、
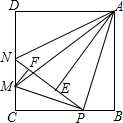 如图,在边长为3的正方形ABCD中,P是BC边上一动点(不含B,C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,连接MA,则AM长度的最小值是$\frac{15}{4}$.
如图,在边长为3的正方形ABCD中,P是BC边上一动点(不含B,C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,连接MA,则AM长度的最小值是$\frac{15}{4}$. 已知,如图,平行四边形ABCD中,AC、BD相交于点O,点E在AD上,点F在CB上,且AE=CF,求证:OE=OF.
已知,如图,平行四边形ABCD中,AC、BD相交于点O,点E在AD上,点F在CB上,且AE=CF,求证:OE=OF.