题目内容
4.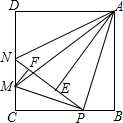 如图,在边长为3的正方形ABCD中,P是BC边上一动点(不含B,C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,连接MA,则AM长度的最小值是$\frac{15}{4}$.
如图,在边长为3的正方形ABCD中,P是BC边上一动点(不含B,C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,连接MA,则AM长度的最小值是$\frac{15}{4}$.
分析 先设PB=x,则CP=3-x,判定△CMP∽△BPA,得出$\frac{PB}{CM}$=$\frac{AB}{PC}$,进而得到CM=$\frac{PB×PC}{AB}$=$\frac{1}{3}$x(3-x),作MG⊥AB于G,根据AM=$\sqrt{M{G}^{2}+A{G}^{2}}$=$\sqrt{{3}^{2}+A{G}^{2}}$,可知AG最小时,AM最小,最后求得AG的最小值,即可得出AM长度的最小值.
解答  解:∵四边形ABCD是正方形,
解:∵四边形ABCD是正方形,
∴AB=CB=DC=AD=3,∠C=∠B=90°,
设PB=x,则CP=3-x,
∵∠APB=∠APE,∠MPC=∠MPN,
∵∠CPN+∠NPB=180°,
∴2∠NPM+2∠APE=180°,
∴∠MPN+∠APE=90°,即∠APM=90°,
∵∠CPM+∠APB=90°,∠APB+∠PAB=90°,
∴∠CPM=∠PAB,
∴△CMP∽△BPA,
∴$\frac{PB}{CM}$=$\frac{AB}{PC}$,
∴CM=$\frac{PB×PC}{AB}$=$\frac{1}{3}$x(3-x),
如图,作MG⊥AB于G,
∵AM=$\sqrt{M{G}^{2}+A{G}^{2}}$=$\sqrt{{3}^{2}+A{G}^{2}}$,
∴AG最小时,AM最小,
∵AG=AB-BG=AB-CM=3-$\frac{1}{3}$x(3-x)=$\frac{1}{3}$(x-$\frac{3}{2}$)2+$\frac{9}{4}$,
∴x=$\frac{3}{2}$时,AG最小值=$\frac{9}{4}$,
∴AM的最小值=$\sqrt{{3}^{2}+(\frac{9}{4})^{2}}$=$\frac{15}{4}$,
故答案为:$\frac{15}{4}$.
点评 本题属于折叠问题,主要考查了正方形的性质、相似三角形的判定和性质、勾股定理以及二次函数的最值等知识的综合应用,解题的关键是构建二次函数解决最值问题,添加常用辅助线构造直角三角形,利用勾股定理进行计算.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案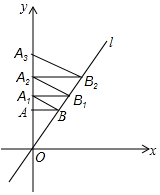 如图,已知直线l的解析式是y=$\sqrt{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,按此作法继续下去,则点A2017的纵坐标为$(\frac{4}{3})^{2017}$.
如图,已知直线l的解析式是y=$\sqrt{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,按此作法继续下去,则点A2017的纵坐标为$(\frac{4}{3})^{2017}$.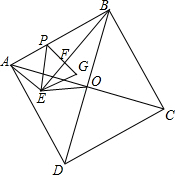 如图,正方形ABCD的边长为$\sqrt{10}$,对角线AC,BD相交于点O,以AB为斜边在正方形内部作Rt△ABE,∠ABE=90°,连接OE,点P为边AB上的一点,将△AEP沿着EP翻折到△GEP,若PG⊥BE于点F,OE=$\sqrt{2}$,则S△EPB=$\frac{3}{2}$-$\frac{3}{20}\sqrt{10}$.
如图,正方形ABCD的边长为$\sqrt{10}$,对角线AC,BD相交于点O,以AB为斜边在正方形内部作Rt△ABE,∠ABE=90°,连接OE,点P为边AB上的一点,将△AEP沿着EP翻折到△GEP,若PG⊥BE于点F,OE=$\sqrt{2}$,则S△EPB=$\frac{3}{2}$-$\frac{3}{20}\sqrt{10}$. 如图,将△ABC沿DE折叠,使得点B与点A重合,△ADC的周长为17cm,AE=5cm,则△ABC的周长为27cm.
如图,将△ABC沿DE折叠,使得点B与点A重合,△ADC的周长为17cm,AE=5cm,则△ABC的周长为27cm.