题目内容
已知△ABC中,AB=AC,∠BAC=α(0°<α<60°),△DBC为等边三角形.
(1)如图1,∠ABD= (用含α的式子表示);
(2)如图2,若∠BCE=150°,∠ABE=60°,判断△ABE的形状,并说明理由;
(3)在(2)的条件下,直线AD与CE的夹角是 ;
(4)在(2)的条件下,若BC=4cm,∠CED=45°,则α= ;AD= cm.

(1)如图1,∠ABD=
(2)如图2,若∠BCE=150°,∠ABE=60°,判断△ABE的形状,并说明理由;
(3)在(2)的条件下,直线AD与CE的夹角是
(4)在(2)的条件下,若BC=4cm,∠CED=45°,则α=

考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)根据等边对等角得出∠ABC=∠ACB,再根据三角形的内角和定理得出∠ABC=90°-
α,最后根据∠DBC=60°,即可得出答案;
(2)连接AD,先证出△ABD≌△ACD,得出∠ADB=∠ADC,再根据∠BDC=60°,求出∠ADB=150°,得出∠ADB=∠BCE,再证出∠ABD=∠EBC,在△ABD和△EBC中,根据ASA得出△ABD≌△EBC,从而得出AB=BE,即可证出△ABE是等边三角形;
(3)先求出∠BCF=30°,根据∠DCB=60°,得出∠DCF=90°,再根据∠ADC=150°,得出∠F=60°即可;
(4)根据已知条件先求出∠DCE=90°,再根据∠DEC=45°,得出△DEC为等腰直角三角形,得出DC=CE=BD=4cm,再根据∠BAD=∠ABD=15°,得出AD=DB=4cm,∠BAC=30°,从而求出α的值.
| 1 |
| 2 |
(2)连接AD,先证出△ABD≌△ACD,得出∠ADB=∠ADC,再根据∠BDC=60°,求出∠ADB=150°,得出∠ADB=∠BCE,再证出∠ABD=∠EBC,在△ABD和△EBC中,根据ASA得出△ABD≌△EBC,从而得出AB=BE,即可证出△ABE是等边三角形;
(3)先求出∠BCF=30°,根据∠DCB=60°,得出∠DCF=90°,再根据∠ADC=150°,得出∠F=60°即可;
(4)根据已知条件先求出∠DCE=90°,再根据∠DEC=45°,得出△DEC为等腰直角三角形,得出DC=CE=BD=4cm,再根据∠BAD=∠ABD=15°,得出AD=DB=4cm,∠BAC=30°,从而求出α的值.
解答:解:(1)∵AB=AC,
∴∠ABC=∠ACB,
∵∠BAC=α,
∴∠ABC=
=90°-
α,
∵△DBC为等边三角形,
∴∠DBC=60°,
∴∠ABD=∠ABC-∠DBC=90°-
α-60°=30°-
α;
故答案为:30°-
α;
(2)△ABE是等边三角形;
如图1,理由如下:连接AD,
∵△DBC为等边三角形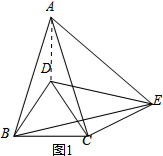 ,
,
∴BD=CD,
∵AB=AC,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠ADB=∠ADC,
∵∠BDC=60°,
∴∠ADB=
=150°,
∴∠ADB=∠BCE,
∵∠ABE=60°,∠DBC=60°,
∴∠ABD=∠EBC,
在△ABD和△EBC中,
,
∴△ABD≌△EBC(ASA),
∴AB=BE,
∴△ABE是等边三角形;
(3)如图2,∵∠BCE=150°,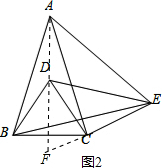
∴∠BCF=30°,
∵∠DCB=60°,
∴∠DCF=90°,
∵∠ADC=150°,
∴∠CDF=30°,
∴∠F=60°;
故答案为:60°;
(4)∵∠BCD=60°,∠BCE=150°,
∴∠DCE=150°-60°=90°,
∵∠DEC=45°,
∴△DEC为等腰直角三角形,
∴DC=CE=BD=4cm,
∵∠BCE=150°,
∴∠BEC=
(180°-150°)=15°,
∴∠BAD=∠ABD=15°,
∴AD=DB=4cm,
∴∠BAC=30°,
∴α=30°.
故答案为:30°,4.
∴∠ABC=∠ACB,
∵∠BAC=α,
∴∠ABC=
| 180-α |
| 2 |
| 1 |
| 2 |
∵△DBC为等边三角形,
∴∠DBC=60°,
∴∠ABD=∠ABC-∠DBC=90°-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:30°-
| 1 |
| 2 |
(2)△ABE是等边三角形;
如图1,理由如下:连接AD,
∵△DBC为等边三角形
 ,
,∴BD=CD,
∵AB=AC,
在△ABD和△ACD中,
|
∴△ABD≌△ACD(SSS),
∴∠ADB=∠ADC,
∵∠BDC=60°,
∴∠ADB=
| 360-60 |
| 2 |
∴∠ADB=∠BCE,
∵∠ABE=60°,∠DBC=60°,
∴∠ABD=∠EBC,
在△ABD和△EBC中,
|
∴△ABD≌△EBC(ASA),
∴AB=BE,
∴△ABE是等边三角形;
(3)如图2,∵∠BCE=150°,

∴∠BCF=30°,
∵∠DCB=60°,
∴∠DCF=90°,
∵∠ADC=150°,
∴∠CDF=30°,
∴∠F=60°;
故答案为:60°;
(4)∵∠BCD=60°,∠BCE=150°,
∴∠DCE=150°-60°=90°,
∵∠DEC=45°,
∴△DEC为等腰直角三角形,
∴DC=CE=BD=4cm,
∵∠BCE=150°,
∴∠BEC=
| 1 |
| 2 |
∴∠BAD=∠ABD=15°,
∴AD=DB=4cm,
∴∠BAC=30°,
∴α=30°.
故答案为:30°,4.
点评:此题主要考查了全等三角形的判定与性质,用到的知识点是等边三角形的性质、全等三角形的判定与性质、三角形的内角和定理,关键是找出全等三角形.

练习册系列答案
相关题目
当地面高于海平面1米时,记作“+1米”,那么地面低于海平面10米时,记作( )
| A、-1米 | B、+1米 |
| C、-10米 | D、+10米 |
已知数a,b在数轴上表示的点的位置如图所示,则下列结论正确的是( )

①a<b<0;②|a|<|b|;③
<0;④b-a>a+b.

①a<b<0;②|a|<|b|;③
| a |
| b |
| A、①② | B、①④ | C、②③ | D、③④ |
 有理数a、b在数轴上对应的位置如图所示,则( )
有理数a、b在数轴上对应的位置如图所示,则( )| A、a+b>0 |
| B、a+b<0 |
| C、a+b=0 |
| D、a-b>0 |
 如图所示,是用直尺和圆规作一个角等于已知角的示意图,则说明∠A′O′B′=∠AOB的依据是( )
如图所示,是用直尺和圆规作一个角等于已知角的示意图,则说明∠A′O′B′=∠AOB的依据是( )| A、SAS | B、SSS |
| C、AAS | D、ASA |
 如图,点A、E、F、C线上,AD∥BC,AD=CB,AE=CE,求证:∠B=∠D.
如图,点A、E、F、C线上,AD∥BC,AD=CB,AE=CE,求证:∠B=∠D. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象,
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象,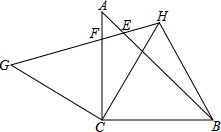 △ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C逆时针旋转角α(0<α<90°)得△GHC,连结BH、CH.CH交AB于点D,GH交AB、AC于点E、点F.
△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C逆时针旋转角α(0<α<90°)得△GHC,连结BH、CH.CH交AB于点D,GH交AB、AC于点E、点F.