题目内容
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象,
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象,(1)求其解析式;
(2)观察图象写出y>0时x的取值范围;
(3)是否存在某直线经过A(1,0)并与该抛物线只有一个公共点?若存在,求出该直线的解析式,若不存在,请说明理由.
考点:待定系数法求二次函数解析式,二次函数的图象,二次函数的性质
专题:计算题
分析:(1)设交点式y=a(x-1)(x-3),然后顶点坐标代入求出a即可;
(2)观察函数图象,找出函数图象在x轴上方所对应的自变量的取值范围即可;
(3)分类讨论:当经过A(1,0)且与y轴平行的直线与该抛物线只有一个公共点,此时易得直线为x=1;当经过A(1,0)的直线y=kx+m与该抛物线只有一个公共点,先把A(1,0)代入y=kx+m得k+m=0,解得m=-k,则直线解析式为y=kx-k,根据抛物线与一次函数的交点问题,得到方程-2x2+8x-6=kx-k有两个相等的实数解,整理得2x2+(k-8)x+6-k=0,则△=(k-8)2-4×2×(6-k)=0,解得k=4,所以经过A(1,0)的直线y=4x-4与该抛物线只有一个公共点.
(2)观察函数图象,找出函数图象在x轴上方所对应的自变量的取值范围即可;
(3)分类讨论:当经过A(1,0)且与y轴平行的直线与该抛物线只有一个公共点,此时易得直线为x=1;当经过A(1,0)的直线y=kx+m与该抛物线只有一个公共点,先把A(1,0)代入y=kx+m得k+m=0,解得m=-k,则直线解析式为y=kx-k,根据抛物线与一次函数的交点问题,得到方程-2x2+8x-6=kx-k有两个相等的实数解,整理得2x2+(k-8)x+6-k=0,则△=(k-8)2-4×2×(6-k)=0,解得k=4,所以经过A(1,0)的直线y=4x-4与该抛物线只有一个公共点.
解答:解:(1)设抛物线解析式为y=a(x-1)(x-3),
把(2,2)代入得a•1•(-1)=2,解得a=-2,
所以抛物线解析式为y=-2(x-1)(x-3)=-2x2+8x-6;
(2)当1<x<3时,y>0;
(3)存在.
当经过A(1,0)的直线为x=1时,直线与该抛物线只有一个公共点;
当经过A(1,0)的直线y=kx+m与该抛物线只有一个公共点,
把A(1,0)代入y=kx+m得k+m=0,解得m=-k,
因为直线y=kx-4与y=-2x2+8x-6只有一个公共点,则方程组
只有一组解,
即-2x2+8x-6=kx-k有两个相等的实数解,
整理得2x2+(k-8)x+6-k=0,△=(k-8)2-4×2×(6-k)=0,解得k=4,
所以经过A(1,0)的直线y=4x-4与该抛物线只有一个公共点,
综上所述,满足条件的直线为x=1或y=4x-4.
把(2,2)代入得a•1•(-1)=2,解得a=-2,
所以抛物线解析式为y=-2(x-1)(x-3)=-2x2+8x-6;
(2)当1<x<3时,y>0;
(3)存在.
当经过A(1,0)的直线为x=1时,直线与该抛物线只有一个公共点;
当经过A(1,0)的直线y=kx+m与该抛物线只有一个公共点,
把A(1,0)代入y=kx+m得k+m=0,解得m=-k,
因为直线y=kx-4与y=-2x2+8x-6只有一个公共点,则方程组
|
即-2x2+8x-6=kx-k有两个相等的实数解,
整理得2x2+(k-8)x+6-k=0,△=(k-8)2-4×2×(6-k)=0,解得k=4,
所以经过A(1,0)的直线y=4x-4与该抛物线只有一个公共点,
综上所述,满足条件的直线为x=1或y=4x-4.
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了二次函数的性质和直线与抛物线的交点问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个多边形的内角和是外角和的3倍,则这个多边形是( )
| A、五边形 | B、六边形 |
| C、七边形 | D、八边形 |
a、b是两个有理数,若a-b<0,那么关于a、b的说法一定正确的是( )
| A、a<0,b<0 |
| B、a<0,b>0 |
| C、a>0,b<0 |
| D、a<b |
某三角形的三个内角之比为6:2:1,该三角形的形状是( )
| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、无法确定 |

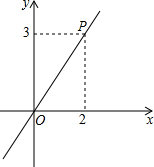 如图,已知正比例函数y=kx经过点P,
如图,已知正比例函数y=kx经过点P,