题目内容
在△ABC中，tanA=1，
，那么△ABC是
- A.钝角三角形
- B.直角三角形
- C.锐角三角形
- D.等腰三角形
A
分析：先根据△ABC中，tanA=1，cotB=
求出∠A及∠B的度数，再由三角形内角和定理求出∠C的度数，进而可判断出三角形的形状．
解答：∵△ABC中，tanA=1，cotB=，
∴∠A=45°，∠B=30°，
∴∠C=180°-∠A-∠B=180°-45°-30°=105°，
∴△ABC是钝角三角形．
故选A．
点评：本题考查的是特殊角的三角函数值及三角形内角和定理，先特殊角的三角函数值求出∠A及∠B的度数是解答此题的关键．
分析：先根据△ABC中，tanA=1，cotB=
求出∠A及∠B的度数，再由三角形内角和定理求出∠C的度数，进而可判断出三角形的形状．解答：∵△ABC中，tanA=1，cotB=
，∴∠A=45°，∠B=30°，
∴∠C=180°-∠A-∠B=180°-45°-30°=105°，
∴△ABC是钝角三角形．
故选A．
点评：本题考查的是特殊角的三角函数值及三角形内角和定理，先特殊角的三角函数值求出∠A及∠B的度数是解答此题的关键．
练习册系列答案
一本好题口算题卡系列答案
相关题目
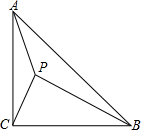如图，在△ABC中，∠ACB=90°，AC=BC，P是△ABC形内一点，且∠APB=∠APC=135°．
在△ABC中，tan∠C=
，AD⊥BC于D，过AC边中点E作EF⊥AB于F，EF交AD于G．
BD；