题目内容
已知实数a是不等于3的常数,解不等式组 ,并依据a的取值情况写出其解集.
,并依据a的取值情况写出其解集.
 当a>3时,不等式组的解集为x≤3;当a<3时,不等式组的解集为x<a.
【解析】试题分析:分别解两个不等式,然后根据不等式组的解集的确定法分情况讨论即可.
试题解析:【解析】
解①得:x≤3,解②得:x<a,
∵实数a是不等于3的常数,
∴当a>3时,不等式组的解集为x≤3;
当a<3时,不等式组的解集为x<a.
当a>3时,不等式组的解集为x≤3;当a<3时,不等式组的解集为x<a.
【解析】试题分析:分别解两个不等式,然后根据不等式组的解集的确定法分情况讨论即可.
试题解析:【解析】
解①得:x≤3,解②得:x<a,
∵实数a是不等于3的常数,
∴当a>3时,不等式组的解集为x≤3;
当a<3时,不等式组的解集为x<a.
练习册系列答案
相关题目
若二次函数y=ax2-2ax+c的图象经过点(-1,0),则方程ax2-2ax+c=0的解为 ( )
A. x1=-3,x2=-1 B. x1=1,x2=3 C. x1=-1,x2=3 D. x1=-3,x2=1
 C
【解析】试题分析:根据题意可得:二次函数的对称轴为直线x=1,则函数与x轴的交点坐标为(-1,0)和(3,0),则方程的解为x=-1或x=3.
C
【解析】试题分析:根据题意可得:二次函数的对称轴为直线x=1,则函数与x轴的交点坐标为(-1,0)和(3,0),则方程的解为x=-1或x=3. 平行四边行的两条对角线把它分成全等三角形的对数是( )
A. 2 B. 4 C. 6 D. 8
 B
【解析】【解析】
如图,?ABCD中,AC,DB分别分得△ABC≌△CDA,△ABD≌△CDB,
又对角线互相平分得到△AOD≌△COB,△AOB≌△COD,所以有4对.
故选B.
B
【解析】【解析】
如图,?ABCD中,AC,DB分别分得△ABC≌△CDA,△ABD≌△CDB,
又对角线互相平分得到△AOD≌△COB,△AOB≌△COD,所以有4对.
故选B. 在□ABCD中,AB≠AD,满足下列条件,不一定能构成平行四边形的是( )
A. 四个内角平分线围成的四边形
B. 过四个顶点作对边的高线围成的四边形
C. 以对角线的交点把对角线分成的四部分的中点为顶点的四边形
D. 以一条对角线上的两点,与另两个顶点为顶点的四边形.
 D
【解析】【解析】
∵?ABCD的四个内角平分线围成的四边形是平行四边形,∴选项A正确;
∵过?ABCD四个顶点作对边的高线围成的四边形是平行四边形,∴选项B正确;
∵以?ABCD各边中点为顶点的四边形是平行四边形,∴选项C正确;
∵以?ABCD一条对角线上的两点与另两个顶点为顶点的四边形不一定是平行四边形,∴选项D不正确.
故选D.
D
【解析】【解析】
∵?ABCD的四个内角平分线围成的四边形是平行四边形,∴选项A正确;
∵过?ABCD四个顶点作对边的高线围成的四边形是平行四边形,∴选项B正确;
∵以?ABCD各边中点为顶点的四边形是平行四边形,∴选项C正确;
∵以?ABCD一条对角线上的两点与另两个顶点为顶点的四边形不一定是平行四边形,∴选项D不正确.
故选D. 下列条件中,能判别四边形是平行四边形的是 ( )
A. 一组对边相等,另一组对边平行 B. 一组对边平行,一组对角互补
C. 一组对角相等,一组邻角互补 D. 一组对角互补,另一组对角相等
 C
【解析】解:A.一组对边相等,另一组对边平行,也有可能是等腰梯形;
B.一组对边平行,一组对角互补,也有可能是等腰梯形;
C.一组对角相等,一组邻角互补可得到两组对角分别相等,所以是平行四边形;
D.一组对角互补,另一组对角相等,可能是含两个直角的一般四边形.
故选C.
C
【解析】解:A.一组对边相等,另一组对边平行,也有可能是等腰梯形;
B.一组对边平行,一组对角互补,也有可能是等腰梯形;
C.一组对角相等,一组邻角互补可得到两组对角分别相等,所以是平行四边形;
D.一组对角互补,另一组对角相等,可能是含两个直角的一般四边形.
故选C. 不等式2x<7的解有_____个,其中非负整数解有___个.
 无数 4
【解析】解不等式2x<7可得x<,所以不等式有无数各界,其中非负整数解有0、1、2、3,共4个.
故答案为:无数,4.
无数 4
【解析】解不等式2x<7可得x<,所以不等式有无数各界,其中非负整数解有0、1、2、3,共4个.
故答案为:无数,4. 下列各式中,是一元一次不等式的是( )
A. 5+4>8 B. 2x-1 C. 2x≤5 D.
D. 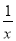 -3x≥0
-3x≥0
 C
【解析】试题解析:A、是不等式,但不是一元一次不等式,故本选项错误;
B、是一元一次方程,不是一元一次不等式,故本选项错误;
C、是一元一次不等式,故本选项正确;
D、不是一元一次不等式,故本选项错误;
故选C.
C
【解析】试题解析:A、是不等式,但不是一元一次不等式,故本选项错误;
B、是一元一次方程,不是一元一次不等式,故本选项错误;
C、是一元一次不等式,故本选项正确;
D、不是一元一次不等式,故本选项错误;
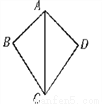
故选C. 如图,在△ABC和△ADC中,下列论断:①AB=AD;②∠ABC=∠ADC=90°;③BC=DC.把其中两个论断作为条件,另一个论断作为结论,可以写出_个真命题.
 2
【解析】根据题意,可得三种命题,由①②③,根据直角三角形全等的判定HL可证明,是真命题;由①③②,能证明∠ABC=∠ADC,但是不能得出一定是90°,是假命题;由②③①,根据SAS可证明两三角形全等,再根据全等三角形的性质可证明,故是真命题.因此可知真命题有2个.
故答案为:2.
2
【解析】根据题意,可得三种命题,由①②③,根据直角三角形全等的判定HL可证明,是真命题;由①③②,能证明∠ABC=∠ADC,但是不能得出一定是90°,是假命题;由②③①,根据SAS可证明两三角形全等,再根据全等三角形的性质可证明,故是真命题.因此可知真命题有2个.
故答案为:2. 某收费站在2 h内对经过该站的机动车统计如下表:
类型 | 轿车 | 货车 | 客车 | 其他 |
数量/辆 | 36 | 24 | 8 | 12 |
若有一辆机动车经过这个收费站,利用上面的统计表估计它是轿车的概率为( )
A.  B.
B. 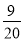 C.
C. 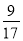 D.
D. 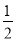
 B
【解析】由图表可得出,轿车的数量为:36,机动车的数量为:36+24+2+12=80,所以轿车的概率为: ,故选:B.
B
【解析】由图表可得出,轿车的数量为:36,机动车的数量为:36+24+2+12=80,所以轿车的概率为: ,故选:B. 
