题目内容
12.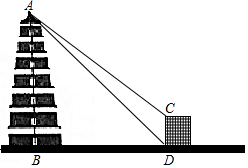 “大雁塔”是西安市的标志性建筑、著名古迹、唐代永徽三年,玄樊为藏经典而修建,塔身七层,被视为古都西安的象征.民间人士道:“不到大雁塔,不算到西安”.小明在学习了锐角三角函数后,想用所学知识测量“大雁塔”的高度,小明在一栋高15米的建筑物底部D处侧得塔顶端A的仰角为45°,接着在建筑物顶端C处测得塔顶端A的仰角为37.5°.已知AB⊥BD,CD⊥BD,请你根据题中提供的相关信息,求出“大雁塔”的高AB的长度.(结果精确到0.1米)(参考数据:sin37.5°≈0.6088,cos37.5°≈0.7934,tan37.5°≈0.7673.
“大雁塔”是西安市的标志性建筑、著名古迹、唐代永徽三年,玄樊为藏经典而修建,塔身七层,被视为古都西安的象征.民间人士道:“不到大雁塔,不算到西安”.小明在学习了锐角三角函数后,想用所学知识测量“大雁塔”的高度,小明在一栋高15米的建筑物底部D处侧得塔顶端A的仰角为45°,接着在建筑物顶端C处测得塔顶端A的仰角为37.5°.已知AB⊥BD,CD⊥BD,请你根据题中提供的相关信息,求出“大雁塔”的高AB的长度.(结果精确到0.1米)(参考数据:sin37.5°≈0.6088,cos37.5°≈0.7934,tan37.5°≈0.7673.
分析 作CE⊥AB于E,则四边形BDCE是矩形,BE=CD=15,设AB=x.根据tan∠ACE=$\frac{AE}{EC}$,列出方程即可解决问题.
解答 解:作CE⊥AB于E. 则四边形BDCE是矩形,BE=CD=15,设AB=x.
则四边形BDCE是矩形,BE=CD=15,设AB=x.
在Rt△ABD中,∵∠ADB=45°,
∴AB=BD=x,
在Rt△AEC中,
tan∠ACE=$\frac{AE}{EC}$,
∴$\frac{x-15}{x}$=0.77,
解得x=65.2米,
答:大雁塔”的高AB的长度为65.2米.
点评 本题考查解直角三角形的应用-仰角俯角问题,锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会用构建方程的思想思考问题.

练习册系列答案
相关题目
17. 如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )
如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )
 如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )
如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )| A. | 130° | B. | 100° | C. | 65° | D. | 50° |
4.下列图形中既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.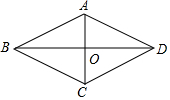 求证:菱形的两条对角线互相垂直.
求证:菱形的两条对角线互相垂直.
已知:如图,四边形ABCD是菱形,对角线AC,BD交于点O.
求证:AC⊥BD.
以下是排乱的证明过程:
①又BO=DO;
②∴AO⊥BD,即AC⊥BD;
③∵四边形ABCD是菱形;
④∴AB=AD.
证明步骤正确的顺序是( )
 求证:菱形的两条对角线互相垂直.
求证:菱形的两条对角线互相垂直.已知:如图,四边形ABCD是菱形,对角线AC,BD交于点O.
求证:AC⊥BD.
以下是排乱的证明过程:
①又BO=DO;
②∴AO⊥BD,即AC⊥BD;
③∵四边形ABCD是菱形;
④∴AB=AD.
证明步骤正确的顺序是( )
| A. | ③→②→①→④ | B. | ③→④→①→② | C. | ①→②→④→③ | D. | ①→④→③→② |