Question

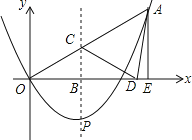
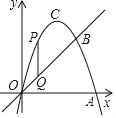
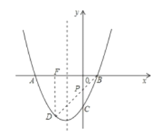
【题目】如图，抛物线与轴交于两点(在的左侧)，与轴交于点， 点与点关于抛物线的对称轴对称.

(1)求抛物线的解析式及点的坐标:

(2)点是抛物线对称轴上的一动点，当的周长最小时，求出点的坐标;

(3)点在轴上，且，请直接写出点的坐标.

Answer 1

【答案】(1) 解析式为，点的坐标为；(2)点的坐标为；(3) 点坐标为或

【解析】

（1）利用待定系数法即可求出n，利用对称性C、D关于对称轴对称即可求出点D坐标．

（2）A，P，D三点在同一直线上时△PAC的周长最小，求出直线AD的解析式即可解决问题．

（3）分两种情形①作DQ∥AC交x轴于点Q，此时∠DQA=∠DAC，满足条件．②设线段AD的垂直平分线交AC于E，直线DE与x的交点为Q′，此时∠Q′DA=′CAD，满足条件，分别求解即可．

解: (1)根据题意得，

解得

抛物线的解析式为

抛物线的对称轴为直线

点与点关于抛物线的对称轴对称

点的坐标为

(2)连接

点与点关于抛物线的对称轴对称.

为定值，

当的值最小

即三点在同一直线上时的周长最小

由解得，

在的左侧，

由两点坐标可求得直线的解析式为

当时，

当的周长最小时，点的坐标为

(3) 点坐标为或