ĢāÄæÄŚČŻ
”¾ĢāÄæ”æijŹŠŠĀ½ØĮĖŌ²ŠĪĪÄ»Æ¹ć³”£¬Š”½ÜŗĶŠ”ŗĘ×¼±ø²»Ķ¬µÄ·½·Ø²āĮæøĆ¹ć³”µÄ°ė¾¶.
£Ø1£©Š”½ÜĻČÕŅŌ²ŠÄ£¬ŌŁĮæ°ė¾¶£¬ĒėÄćŌŚĶ¼1ÖŠ£¬ÓĆ³ß¹ę×÷Ķ¼µÄ·½·Ø°ļŠ”½ÜÕŅµ½øĆ¹ć³”µÄŌ²ŠÄ![]() £Ø²»Š“×÷·Ø£¬±£Įō×÷Ķ¼ŗŪ¼££©£»
£Ø²»Š“×÷·Ø£¬±£Įō×÷Ķ¼ŗŪ¼££©£»
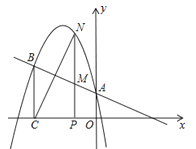
£Ø2£©Š”ŗĘŌŚ¹ć³”±ß£ØČēĶ¼2£©Ń”Č”![]() ”¢
Ӣ![]() Ӣ
”¢![]() ČżøłŹÆÖł£¬ĮæµĆ
ČżøłŹÆÖł£¬ĮæµĆ![]() ”¢
”¢![]() Ö®¼äµÄ¾ąĄėÓė
Ö®¼äµÄ¾ąĄėÓė![]() ”¢
”¢![]() Ö®¼äµÄ¾ąĄėĻąµČ£¬²¢²āµĆ
Ö®¼äµÄ¾ąĄėĻąµČ£¬²¢²āµĆ![]() ³¤ĪŖ240Ć×£¬
³¤ĪŖ240Ć×£¬![]() µ½
µ½![]() µÄ¾ąĄėĪŖ5Ć×.ĒėÄć°ļĖūĒó³ö¹ć³”µÄ°ė¾¶£»
µÄ¾ąĄėĪŖ5Ć×.ĒėÄć°ļĖūĒó³ö¹ć³”µÄ°ė¾¶£»
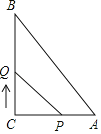
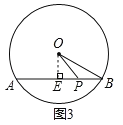
£Ø3£©ĒėÄć½ā¾öĻĀĆęµÄĪŹĢā£ŗČēĶ¼3£¬![]() µÄÖ±¾¶ĪŖ
µÄÖ±¾¶ĪŖ![]() £¬ĻŅ
£¬ĻŅ![]() £¬
£¬![]() ŹĒĻŅ
ŹĒĻŅ![]() ÉĻµÄŅ»øö¶Æµć£¬Ēó³ö
ÉĻµÄŅ»øö¶Æµć£¬Ēó³ö![]() µÄ³¤¶Č·¶Ī§ŹĒ¶ąÉŁ£æ
µÄ³¤¶Č·¶Ī§ŹĒ¶ąÉŁ£æ
”¾“š°ø”æ£Ø1£©Ļź¼ū½āĪö£»£Ø2£©¹ć³”µÄ°ė¾¶1443Ć×£»£Ø3£©![]() .
.
”¾½āĪö”æ
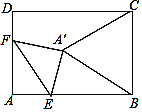
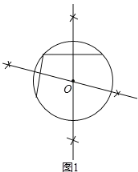
£Ø1£©×÷³öĻŅµÄ“¹Ö±Ę½·ÖĻߣ¬ŌŁ½įŗĻ“¹¾¶¶ØĄķĶĘĀŪµĆ³öŌ²ŠÄĪ»ÖĆ£»
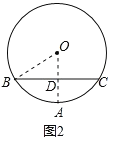
£Ø2£©ÉčŌ²ŠÄĪŖO£¬Į¬½į OA”¢OB£¬OA½»BCÓŚD£¬øł¾ŻA”¢BÖ®¼äµÄ¾ąĄėÓėA”¢CÖ®¼äµÄ¾ąĄėĻąµČ£¬µĆ³ö![]() £¬“Ó¶ųµĆ³öBD=DC=
£¬“Ó¶ųµĆ³öBD=DC=![]() BC£¬ŌŁøł¾Ż¹“¹É¶ØĄķµĆ³öOB2=OD2+BD2£¬ÉčOB=x£¬¼“æÉĒó³ö¹ć³”µÄ°ė¾¶£»
BC£¬ŌŁøł¾Ż¹“¹É¶ØĄķµĆ³öOB2=OD2+BD2£¬ÉčOB=x£¬¼“æÉĒó³ö¹ć³”µÄ°ė¾¶£»
£Ø3£©¹żµćO×÷OE”ĶABÓŚµćE£¬Į¬½ÓOB£¬ÓÉ“¹¾¶¶ØĄķæÉÖŖAE=BE=![]() AB£¬ŌŁøł¾Ż¹“¹É¶ØĄķĒó³öOEµÄ³¤£¬ÓÉ“ĖæÉµĆ³ö½įĀŪ£®
AB£¬ŌŁøł¾Ż¹“¹É¶ØĄķĒó³öOEµÄ³¤£¬ÓÉ“ĖæÉµĆ³ö½įĀŪ£®
½ā£ŗČēĶ¼1ĖłŹ¾£¬ŌŚŌ²ÖŠ×÷ČĪŅā2ĢõĻŅµÄ“¹Ö±Ę½·ÖĻߣ¬ÓÉ“¹¾¶¶ØĄķæÉÖŖÕā2Ģõ“¹Ö±Ę½·ÖĻß±Ų¶ØÓėŌ²µÄ2ĢõÖ±¾¶ÖŲŗĻ£¬ĖłŅŌ½»µć![]() ¼“ĪŖĖłĒó£»
¼“ĪŖĖłĒó£»
£Ø2£©ČēĶ¼2£¬Į¬½į![]() ”¢
”¢![]() £¬
£¬![]() ½»
½»![]() ÓŚ
ÓŚ![]() £¬
£¬
”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £ØĆ×£©£¬
£ØĆ×£©£¬
ÓÉĢāŅā![]() £¬
£¬
ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬
Éč![]() £¬Ōņ
£¬Ōņ![]() £¬
£¬
½āµĆ£ŗ![]() £¬
£¬
![]() £¬
£¬
”ą¹ć³”µÄ°ė¾¶1443Ć×.
£Ø3£©ČēĶ¼3£¬¹żµć![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬
£¬
”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ß![]() µÄÖ±¾¶ĪŖ
µÄÖ±¾¶ĪŖ![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ß“¹Ļ߶Ī×ī¶Ģ£¬°ė¾¶×ī³¤£¬
”ą![]() .
.

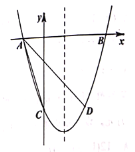
”¾ĢāÄæ”æ±ķÖŠĖłĮŠ ![]() µÄ7¶ŌÖµŹĒ¶ž“ĪŗÆŹż
µÄ7¶ŌÖµŹĒ¶ž“ĪŗÆŹż![]() Ķ¼ĻóÉĻµÄµćĖł¶ŌÓ¦µÄ×ų±ź£¬ĘäÖŠ
Ķ¼ĻóÉĻµÄµćĖł¶ŌÓ¦µÄ×ų±ź£¬ĘäÖŠ ![]()
x | ” |
|
|
|
|
|
|
| ” |
y | ” | 7 | m | 14 | k | 14 | m | 7 | ” |
øł¾Ż±ķÖŠĢį¹©µÄŠÅĻ¢£¬ÓŠŅŌĻĀ4 øöÅŠ¶Ļ£ŗ
¢Ł ![]() £»¢Ś
£»¢Ś ![]() £»¢Ū µ±
£»¢Ū µ±![]() Ź±£¬y µÄÖµŹĒ k£»¢Ü
Ź±£¬y µÄÖµŹĒ k£»¢Ü ![]() ĘäÖŠÅŠ¶ĻÕżČ·µÄŹĒ £Ø £©
ĘäÖŠÅŠ¶ĻÕżČ·µÄŹĒ £Ø £©
A. ¢Ł¢Ś¢Ū B. ¢Ł¢Ś¢Ü C. ¢Ł¢Ū¢Ü D. ¢Ś¢Ū¢Ü