Question

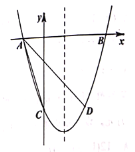
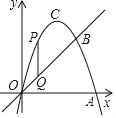
【题目】如图，在平面直角坐标系xOy中，抛物线顶点为C（1，2），且与直线y＝x交于点B（，）；点P为抛物线上O，B两点之间一个动点（不与O，B两点重合），过P作PQ∥y轴交线段OB于点Q．

（1）求抛物线的解析式；

（2）当PQ的长度为最大值时，求点Q的坐标；

（3）点M为抛物线上O，B两点之间一个动点（不与O，B两点重合），点N为线段OB上一个动点；当四边形PQNM为平行四边形，且PN⊥OB时，请直接写出Q点坐标．

Answer 1

【答案】（1）y＝﹣2x2+4x；（2）当PQ的长度为最大值时，点Q的坐标为（，）；（3）点Q的坐标为（，）

【解析】

（1）由抛物线的顶点坐标设出抛物线的解析式为y＝a（x﹣1）2+2（a≠0），代入点B的坐标即可求出a值，进而可得出抛物线的解析式；

（2）设点P的坐标为（x，﹣2x2+4x）（0＜x＜），则点Q的坐标为（x，x），进而可得出PQ＝﹣2x2+3x，再利用二次函数的性质即可解决最值问题；

（3）设点Q的坐标为（m，m），点N的坐标为（n，n），则点P的坐标为（m，﹣2m2+4m），点M的坐标为（n，﹣2n2+4n），根据平行四边形的性质可得出m+n＝，由PN⊥OB及直线OB的解析式可得出△PNQ为等腰直角三角形，根据等腰直角三角形的性质可得出PQ＝2（n﹣m），结合PQ＝﹣2m2+3m，m+n＝，即可得出关于m的一元二次方程，解之取大于0小于的值即可得出结论．

解：（1）∵抛物线顶点为C（1，2），

∴设抛物线的解析式为y＝a（x﹣1）2+2（a≠0）．

∵点B（，）在抛物线上，

∴＝a（﹣1）2+2，

∴a＝﹣2，

∴抛物线的解析式为y＝﹣2（x﹣1）2+2，即y＝﹣2x2+4x．

（2）设点P的坐标为（x，﹣2x2+4x）（0＜x＜），则点Q的坐标为（x，x），

∴PQ＝﹣2x2+4x﹣x＝﹣2x2+3x＝﹣2（x﹣）2+．

∵﹣2＜0，

∴当x＝时，PQ的长度取最大值，

∴当PQ的长度为最大值时，点Q的坐标为（，）．

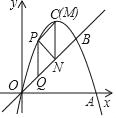
（3）依照题意画出图形，如图所示．

设点Q的坐标为（m，m），点N的坐标为（n，n），则点P的坐标为（m，﹣2m2+4m），点M的坐标为（n，﹣2n2+4n），

∴PQ＝﹣2m2+3m，MN＝﹣2n2+3n．

∵四边形PQNM为平行四边形，

∴PQ＝MN，即﹣2m2+3m＝﹣2n2+3n，

∴﹣2（m+n）（m﹣n）+3（m﹣n）＝0．

∵m≠n，

∴m+n＝，

∴n＝﹣m．

∵直线OB的解析式为y＝x，PN⊥OB，

∴△PNQ为等腰直角三角形，

∴PQ＝NQ＝2（n﹣m），即﹣2m2+3m＝3﹣4m，

整理得：2m2﹣7m+3＝0，

解得：m1＝，m2＝3（不合题意，舍去），

∴点Q的坐标为（，）．