题目内容
超市有一种“喜之郎”果冻礼盒,内装两个上下倒置的果冻,果冻高为3cm,底面是一个直径为4cm的圆,横断面可以近似地看作是一个抛物线,为了节约成本,包装应尽可能地小.请计算制作这样一个包装盒至少需要纸张多少平方厘米?(不计重合的部分)
考点:二次函数的应用
专题:
分析:如图,“喜之郎”果冻礼盒是一长方体.底面为矩形A′B′C′D′(如图3),侧面为矩形ABCD(如图2).
解答: 解:建立如图(2)所示的平面直角坐标系,过切点K作KH⊥OD于点H.
解:建立如图(2)所示的平面直角坐标系,过切点K作KH⊥OD于点H.
依题意知 K(x,
).
易求开口向上抛物线的解析式:y=
x2,
所以 当
=
x2,
解得 x=
或x=-
(舍去),
∴OH=HG=
,
∴BC=BO+OH+HG+GC=2+2
+2=4+2
,
∴S矩形ABCD=AB•BC=3×(4+2
)=12+6
(平方厘米).
如图3,S矩形A′B′C′D′=AB•BC=4×(4+2
)=16+8
(平方厘米).
所以,2S矩形ABCD+2S矩形A′B′C′D′+2×3×4=28
+80(平方厘米).
答:一个包装盒至少需要纸张(80+28
)平方厘米.
 解:建立如图(2)所示的平面直角坐标系,过切点K作KH⊥OD于点H.
解:建立如图(2)所示的平面直角坐标系,过切点K作KH⊥OD于点H.依题意知 K(x,
| 3 |
| 2 |
易求开口向上抛物线的解析式:y=
| 3 |
| 4 |
所以 当
| 3 |
| 2 |
| 3 |
| 4 |
解得 x=
| 2 |
| 2 |
∴OH=HG=
| 2 |
∴BC=BO+OH+HG+GC=2+2
| 2 |
| 2 |
∴S矩形ABCD=AB•BC=3×(4+2
| 2 |
| 2 |
如图3,S矩形A′B′C′D′=AB•BC=4×(4+2
| 2 |
| 2 |
所以,2S矩形ABCD+2S矩形A′B′C′D′+2×3×4=28
| 2 |
答:一个包装盒至少需要纸张(80+28
| 2 |
点评:本题考查了二次函数的应用.此题采用逆向思维,通过补全图形来计算包装盒的表面积.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 如图,以等腰直角△ABC两锐角顶点A,B为圆心作等圆,⊙A与⊙B恰好外切,若AC=2,那么图中两个扇形(即阴影部分)的面积之和为( )
如图,以等腰直角△ABC两锐角顶点A,B为圆心作等圆,⊙A与⊙B恰好外切,若AC=2,那么图中两个扇形(即阴影部分)的面积之和为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列三对数值中:
①
;②
;③
.
是方程2x-y=4的解的是( )
①
|
|
|
是方程2x-y=4的解的是( )
| A、① | B、② | C、③ | D、①③ |
 一个由棱长都是1的小正方体组成的立体图形的三视图如图,则它的表面积为( )
一个由棱长都是1的小正方体组成的立体图形的三视图如图,则它的表面积为( )| A、10 | B、12 | C、14 | D、20 |
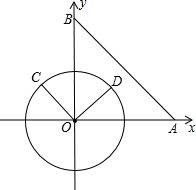 在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中C、O、D按逆时针方向排列),连接AB.
在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中C、O、D按逆时针方向排列),连接AB.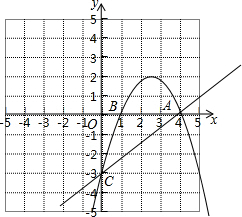 已知抛物线y=-
已知抛物线y=- 如图,直线AB、CD被直线EF所截,如果同位角∠1=∠3,那么内错角∠2与∠3相等吗?同旁内角∠3与∠5互补吗?请说明理由.
如图,直线AB、CD被直线EF所截,如果同位角∠1=∠3,那么内错角∠2与∠3相等吗?同旁内角∠3与∠5互补吗?请说明理由. 如图,△ABC中,AB=AC,D是△ABC内一点,连接AD、BD、CD,∠ADB=∠ADC,求证:DB=DC.
如图,△ABC中,AB=AC,D是△ABC内一点,连接AD、BD、CD,∠ADB=∠ADC,求证:DB=DC.