题目内容
 已知抛物线y=-
已知抛物线y=-| 3 |
| 4 |
| 15 |
| 4 |
考点:抛物线与x轴的交点
专题:计算题
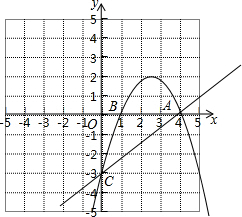
分析:根据抛物线解析式求出A,B,C坐标,确定出直线AC解析式,当一条直线与直线AC平行,且与抛物线只有一个交点D时,三角形ACD面积最大,设出直线解析式,与抛物线解析式联立消去y,得到关于x的一元二次方程,且根的判别式等于0,求出m的值,即可确定出此时D的坐标.
解答:解:对于抛物线y=-
x2+
x-3,
令y=0,得到-
x2+
x-3=0,
解得:x=1或x=4,
∴B(1,0),A(4,0),
令x=0,得到y=-3,即C(0,-3),
设直线AC解析式为y=kx+b,
将A与C坐标代入得:
,
解得:k=
,b=-3,
∴直线AC解析式为y=
x-3,
设平行于直线AC,且与抛物线只有一个交点的直线方程为y=
x+m,
此时直线与抛物线交于点D,使得△ACD的面积最大,
与二次函数解析式联立消去y得:-
x2+
x-3=
x+m,
整理得:3x2-12x+4m+12=0,
∴△=144-12(4m+12)=0,
解得:m=0,
∴此时直线方程为y=
x,点D坐标为(2,
).
| 3 |
| 4 |
| 15 |
| 4 |
令y=0,得到-
| 3 |
| 4 |
| 15 |
| 4 |
解得:x=1或x=4,
∴B(1,0),A(4,0),
令x=0,得到y=-3,即C(0,-3),
设直线AC解析式为y=kx+b,
将A与C坐标代入得:
|
解得:k=
| 3 |
| 4 |
∴直线AC解析式为y=
| 3 |
| 4 |
设平行于直线AC,且与抛物线只有一个交点的直线方程为y=
| 3 |
| 4 |
此时直线与抛物线交于点D,使得△ACD的面积最大,
与二次函数解析式联立消去y得:-
| 3 |
| 4 |
| 15 |
| 4 |
| 3 |
| 4 |
整理得:3x2-12x+4m+12=0,
∴△=144-12(4m+12)=0,
解得:m=0,
∴此时直线方程为y=
| 3 |
| 4 |
| 3 |
| 4 |
点评:此题考查了抛物线与x轴的交点,两直线平行时斜率满足的关系,解题的关键是:“平行于直线AC,且与抛物线只有一个交点的直线方程与抛物线交点为D,使得△ACD的面积最大”.

练习册系列答案
相关题目
下列计算正确的是( )
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
解方程
-
=
,去分母所得结论正确的是( )
| x+3 |
| 3 |
| x-1 |
| 6 |
| 5-x |
| 2 |
| A、x+3-x+1=15-x |
| B、2x+6-x+1=15-3x |
| C、x+6-x-1=15-x |
| D、x+3-x+1=15-3x |
 如图,在平面直角坐标系中,已知四边形ABCD的四个顶点坐标为A(0,6)、B(-3,0)、C(0,-2)、D(4,0),P为AB、DC延长线的交点.
如图,在平面直角坐标系中,已知四边形ABCD的四个顶点坐标为A(0,6)、B(-3,0)、C(0,-2)、D(4,0),P为AB、DC延长线的交点. 已知,AB、AC是圆O的切线,B、C是切点,BD是圆O的直径,连接AO、CD,
已知,AB、AC是圆O的切线,B、C是切点,BD是圆O的直径,连接AO、CD, 如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为
如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为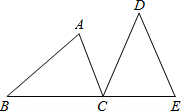 如图,△ABC由△EDC绕C点旋转得到,B、C、E三点在同一条直线上,∠ACD=∠B.求证:△ABC是等腰三角形.
如图,△ABC由△EDC绕C点旋转得到,B、C、E三点在同一条直线上,∠ACD=∠B.求证:△ABC是等腰三角形.