Question

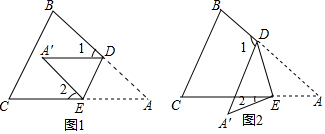
3．把一张纸片△ABC对折，折痕为DE．
（1）如图1，若点A落在四边形BCED的内部点A′处，求证：∠1+∠2=2∠A；
（2）如图2，若点A落在四边形BCED的外部点A′处，则∠1、∠2与∠A又满足怎样的数量关系？写出这个数量关系，并给出证明．

Answer 1

分析 （1）根据翻折的性质表示出∠3、∠4，再根据三角形的内角和定理列式整理即可得解；
（2）先根据翻折的性质以及平角的定义表示出∠3、∠4，再根据三角形的内角和定理列式整理即可得解．

解答 解：（1）如图，根据翻折的性质，∠3=$\frac{1}{2}$（180-∠1），∠4=$\frac{1}{2}$（180-∠2），
∵∠A+∠3+∠4=180°，
∴∠A+$\frac{1}{2}$（180-∠1）+$\frac{1}{2}$（180-∠2）=180°，
整理得，2∠A=∠1+∠2；

（2）根据翻折的性质，∠3=$\frac{1}{2}$（180-∠1），∠4=$\frac{1}{2}$（180+∠2），
∵∠A+∠3+∠4=180°，
∴∠A+$\frac{1}{2}$（180-∠1）+$\frac{1}{2}$（180+∠2）=180°，
整理得，2∠A=∠1-∠2．

点评 本题主要考查了三角形的内角和定理，多边形的内角与外角，翻折的性质，整体思想的利用是解题的关键．