题目内容
11. 如图,BA⊥MN,BA=2$\sqrt{3}$,点P是射线AN上的一个动点(点P与点A不重合),∠BPC=∠BPA,BC⊥BP,过点C作CD⊥MN,垂足为D,在P点运动过程中,当AP=2或6时,△ABP和△CDP相似.
如图,BA⊥MN,BA=2$\sqrt{3}$,点P是射线AN上的一个动点(点P与点A不重合),∠BPC=∠BPA,BC⊥BP,过点C作CD⊥MN,垂足为D,在P点运动过程中,当AP=2或6时,△ABP和△CDP相似.
分析 当△BAP∽△CDP时,易得∠BPA=60°,AP=$\frac{BA}{tan60°}$=$\frac{2\sqrt{3}}{\sqrt{3}}$,当△BAP∽△PDC时,易得∠BPA=30°,AP=$\frac{BA}{tan30°}$=6.
解答  解:如图1,当△BAP∽△CDP时,
解:如图1,当△BAP∽△CDP时,
∵∠BPC=∠BPA,∠CPD=∠BPA,
∴∠BPA=∠BPC=∠CPD=60°,
∴AP=$\frac{BA}{tan60°}$=$\frac{2\sqrt{3}}{\sqrt{3}}$=2
如图2,当△BAP∽△PDC时,
∵∠CPB=∠BPA,∠PCD=∠BPA,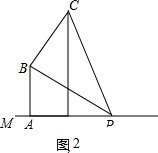
∴3∠BPA=90°,
∴∠BPA=30°,
∴AP=$\frac{BA}{tan30°}$=6.
所以AP=2或AP=6时,△ABP和△CDP相似;
故答案是:2或6.
点评 此题主要考查了相似三角形的判定与性质和锐角三角函数关系等知识,熟练利用相似三角形的性质得出线段之间的关系是解题关键.

练习册系列答案
相关题目
2. 如图,已知AB=AC=AD,∠BAC=50°,∠DAC=30°,则∠CBD的度数为( )
如图,已知AB=AC=AD,∠BAC=50°,∠DAC=30°,则∠CBD的度数为( )
 如图,已知AB=AC=AD,∠BAC=50°,∠DAC=30°,则∠CBD的度数为( )
如图,已知AB=AC=AD,∠BAC=50°,∠DAC=30°,则∠CBD的度数为( )| A. | 15° | B. | 25° | C. | 50° | D. | 65° |
19.下列事件是确定事件的是( )
| A. | 抛出一枚硬币,落地后正面朝上 | |
| B. | 明天会下雨 | |
| C. | 打开电视机,正在播放“爸爸去哪”节目 | |
| D. | 实心铁球投入水中会沉入水底 |
6.若分式$\frac{x+2}{x-2}$的值为零,则x等于( )
| A. | 0 | B. | 2 | C. | -2 | D. | ±2 |
1. 小红随意在如图所示的地板上踢毽子,则毽子恰落在黑色方砖上的概率为( )
小红随意在如图所示的地板上踢毽子,则毽子恰落在黑色方砖上的概率为( )
 小红随意在如图所示的地板上踢毽子,则毽子恰落在黑色方砖上的概率为( )
小红随意在如图所示的地板上踢毽子,则毽子恰落在黑色方砖上的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{25}$ |
 如图,在?ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠EAB的度数为50°.
如图,在?ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠EAB的度数为50°. 如图,一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反比例函数y=-$\frac{8}{x}$的图象在第二象限交于点C,如果点A的坐标为(2,0),B是AC的中点,则该一次函数的解析式是y=-x+2.
如图,一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反比例函数y=-$\frac{8}{x}$的图象在第二象限交于点C,如果点A的坐标为(2,0),B是AC的中点,则该一次函数的解析式是y=-x+2.