题目内容
13.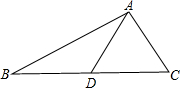 如图,AD是△ABC的中线,将△ABD绕点D旋转180°得到△ECD,若AB=15,AC=8,则:
如图,AD是△ABC的中线,将△ABD绕点D旋转180°得到△ECD,若AB=15,AC=8,则:(1)BC的取值范围为7<BC<23;
(2)AE的取值范围为7<AE<23;
(3)AD的取值范围为$\frac{7}{2}$<AD<$\frac{23}{2}$.
分析 (1)直接根据三角形的三边关系求出BC的取值范围即可;
(2)根据图形旋转的性质得出AD=DE,CE=AB,再由三角形的三边关系可得出结论;
(3)先根据SAS定理得出△ABD≌△ECD,故CE=AB.在△ACE中,根据三角形的三边关系即可得出结论.
解答  解:(1)在△ABC中,
解:(1)在△ABC中,
∵AB=15,AC=8,
∴AB-AC<BC<AB+AC,即15-8<BC<15+8,解得7<BC<23.
故答案为:7,23;
(2)∵△ECD由△旋转而成,
∴AB=CE=15.
在△ACE中,
∵AC=8,CE=15,
∴CE-AC<AE<CE+AC,即15-8<AE<15+8,即7<AE<23.
故答案为:7,23;
(3)在△ABD与△ECD中,
$\left\{\begin{array}{l}BD=CD\\∠ADB=∠EDC\\ AD=DE\end{array}\right.$,
∴△ABD≌△ECD(SAS),
∴CE=AB.
在△ACE中,CE-AC<AE<CE+AC,即7<2AD=AE<23,
∴$\frac{7}{2}$<AD<$\frac{23}{2}$.
故答案为:$\frac{7}{2}$,$\frac{23}{2}$.
点评 本题考查的是三角形的三边关系,熟知三角形任意两边之和大于第三边,任意两边差小于第三边是解答此题的关键.

练习册系列答案
相关题目
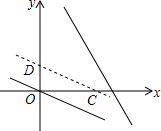 已知:点P是一次函数y=-3x+6图象在y右轴侧部分上的一个动点,将直线y=-$\frac{1}{2}$x沿y轴向上平移,分别交x轴,y轴于C、D两点.
已知:点P是一次函数y=-3x+6图象在y右轴侧部分上的一个动点,将直线y=-$\frac{1}{2}$x沿y轴向上平移,分别交x轴,y轴于C、D两点. 已知∠BAE=∠EAC,∠ACD=∠B,图中共有几对相似三角形?说明理由.
已知∠BAE=∠EAC,∠ACD=∠B,图中共有几对相似三角形?说明理由.