题目内容
20.(1)一次函数y=2x-a与x轴的交点是点(-2,0)关于y轴的对称点,求一元一次不等式2x-a≤0的解集.(2)已知2a-3x+1=0,3b-2x-16=0,且a≤4<b,求x的取值范围.
分析 (1)先根据点关于y轴对称的坐标特点得到一次函数y=2x-a与x轴的交点是(2,0),把(2,0)代入解析式可求出a得值,然后把a得值代入2x-a≤0,再解不等式即可;
(2)根据已知等式得a=$\frac{3x-1}{2}$,b=$\frac{2x+16}{3}$,代入a≤4<b中,解不等式组即可.
解答 解:(1)∵(-2,0)关于y轴得对称点为(2,0),
把(2,0)在y=2x-a得0=4-a,解得a=4.
当a=4时,2x-4≤0,解得x≤2;
(2)依题意,得a=$\frac{3x-1}{2}$,b=$\frac{2x+16}{3}$,
代入a≤4<b中,得$\left\{\begin{array}{l}{\frac{3x-1}{2}≤4}\\{\frac{2x+16}{3}>4}\end{array}\right.$,解得$\left\{\begin{array}{l}{x≤3}\\{x>-2}\end{array}\right.$,
∴不等式组的解集为:-2<x≤3.
点评 本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
相关题目
10.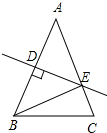 在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若∠EBC=30°,则∠A的度数为( )
在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若∠EBC=30°,则∠A的度数为( )
 在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若∠EBC=30°,则∠A的度数为( )
在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若∠EBC=30°,则∠A的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
8.下面的多项式中,能因式分解的是( )
| A. | m2+(-n)2 | B. | m2-m+1 | C. | m2-n | D. | m2-2m+1 |
9.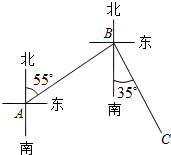 如图所示,一个人从A点出发,沿着北偏东55°方向走到B点,再从点B出发沿着南偏东35°方向走到C点,则∠ABC的度数为( )
如图所示,一个人从A点出发,沿着北偏东55°方向走到B点,再从点B出发沿着南偏东35°方向走到C点,则∠ABC的度数为( )
 如图所示,一个人从A点出发,沿着北偏东55°方向走到B点,再从点B出发沿着南偏东35°方向走到C点,则∠ABC的度数为( )
如图所示,一个人从A点出发,沿着北偏东55°方向走到B点,再从点B出发沿着南偏东35°方向走到C点,则∠ABC的度数为( )| A. | 20° | B. | 90° | C. | 70° | D. | 125° |
10. 实数a在数轴上的位置如图所示,则$\sqrt{(a-2)^{2}}$+$\sqrt{(a-7)^{2}}$化简后为( )
实数a在数轴上的位置如图所示,则$\sqrt{(a-2)^{2}}$+$\sqrt{(a-7)^{2}}$化简后为( )
 实数a在数轴上的位置如图所示,则$\sqrt{(a-2)^{2}}$+$\sqrt{(a-7)^{2}}$化简后为( )
实数a在数轴上的位置如图所示,则$\sqrt{(a-2)^{2}}$+$\sqrt{(a-7)^{2}}$化简后为( )| A. | 5 | B. | -5 | C. | 2a-9 | D. | 2a+5 |
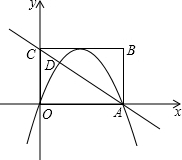 如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=8,OC=6,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.
如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=8,OC=6,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.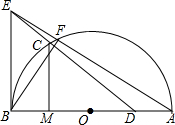 如图,在半径为2的⊙O中,AB是直径,C是弧AB的三等分点(∠BOC为锐角),D是OA的中点,BE是⊙O的切线,B为切点,DC的延长线交BE于点E,连接AE,交⊙O于点F.
如图,在半径为2的⊙O中,AB是直径,C是弧AB的三等分点(∠BOC为锐角),D是OA的中点,BE是⊙O的切线,B为切点,DC的延长线交BE于点E,连接AE,交⊙O于点F.