题目内容
方程组
有两组相同的实数解,则k是( )
|
| A、k>1 | B、k<1 |
| C、k=1 | D、k=-1 |
考点:根的判别式
专题:
分析:首先运用代入消元法得到关于x的方程,再根据方程组有两个相同的实数解,则此方程应有两个相等的实数根,根据△=0即可求得k的值.
解答:解:
①代入②,整理得x2-2x-k=0,
根据题意,有△=4+4k=0,
解得k=-1.
故选D.
|
①代入②,整理得x2-2x-k=0,
根据题意,有△=4+4k=0,
解得k=-1.
故选D.
点评:本题主要考查了一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列事件是必然事件的是 ( )
A、方程
| ||||
B、方程
| ||||
| C、方程x4-1=0有实数根 | ||||
| D、方程3x2=x只有一个实数根 |
 如图,在函数y1=
如图,在函数y1=| k1 |
| x |
| k2 |
| x |
| 3 |
| 2 |
| 27 |
| 2 |
| A、8 | B、9 | C、10 | D、11 |
计算(-
)-1的倒数为( )
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
 如图,AB∥CD,AF与CD交于点E,BE⊥AF,∠B=60°,则∠DEF的度数是( )
如图,AB∥CD,AF与CD交于点E,BE⊥AF,∠B=60°,则∠DEF的度数是( )| A、10° | B、20° |
| C、30° | D、40° |
下列说法不正确的是( )
| A、有理数和无理数统称为实数 |
| B、无理数是无限不循环小数 |
| C、无理数包括正无理数、零、负无理数 |
| D、无理数都可以用数轴上的点来表示 |
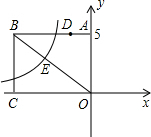 如图,矩形ABCO的两边OC、OA分别位于x轴、y轴上,点B的坐标为(-
如图,矩形ABCO的两边OC、OA分别位于x轴、y轴上,点B的坐标为(-


