题目内容
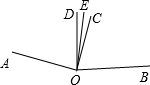 如图,已知∠AOB=165°,AO⊥OC,DO⊥OB,OE平分∠COD,求∠COE的度数.
如图,已知∠AOB=165°,AO⊥OC,DO⊥OB,OE平分∠COD,求∠COE的度数.考点:垂线,角平分线的定义
专题:
分析:由AO⊥OC,可得∠AOC=90°,由∠BOC=∠AOB-∠AOC,所以∠BOC=75°,又因为DO⊥OB,可得∠BOD=90°,由∠DOC=∠BOD-∠BOC,所以∠DOC=15°,然后由OE平分∠COD,所以∠COE=
∠COD=7.5°.
| 1 |
| 2 |
解答:解:∵AO⊥OC,
∴∠AOC=90°,
∵∠AOB=165°,
∴∠BOC=∠AOB-∠AOC=165°-90°=75°,
∵DO⊥OB,
∴∠BOD=90°,
∴∠DOC=∠DOB-∠BOC=90°-75°=15°,
∵OE平分∠COD,
∴∠COE=
∠COD=
×15°=7.5°.
∴∠AOC=90°,
∵∠AOB=165°,
∴∠BOC=∠AOB-∠AOC=165°-90°=75°,
∵DO⊥OB,
∴∠BOD=90°,
∴∠DOC=∠DOB-∠BOC=90°-75°=15°,
∵OE平分∠COD,
∴∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了垂线的性质、角平分线的性质及角的计算,正确理解垂线的性质、角平分线的性质是解题的关键.

练习册系列答案
相关题目

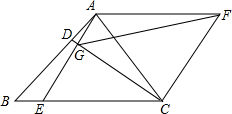 如图,△ABC和△ACF均为等边三角形,点D、E分别为AD,BE边上的点,且AD=BE,AE与CD交于G点,连接GF.
如图,△ABC和△ACF均为等边三角形,点D、E分别为AD,BE边上的点,且AD=BE,AE与CD交于G点,连接GF. 如图的几何体由棱长为1厘米的正方体组成.
如图的几何体由棱长为1厘米的正方体组成. 如图,已知△ABC为等边三角形,O为其内部一点,将△AOC绕点A旋转60°得到△ADB,连接OD,DB,已知AO=3cm,BO=5cm,CO=4cm,求△ODB的周长.
如图,已知△ABC为等边三角形,O为其内部一点,将△AOC绕点A旋转60°得到△ADB,连接OD,DB,已知AO=3cm,BO=5cm,CO=4cm,求△ODB的周长. 如图所示,用两个钢索加固直立的电线杆,若要使AB与AC的长相等,需添加条件
如图所示,用两个钢索加固直立的电线杆,若要使AB与AC的长相等,需添加条件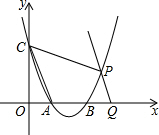 如图,抛物线y=x2-3x+2与x轴交于A,B两点,与y轴交于点C,连接AC,将直线AC向右平移交抛物线于点P,交x轴于Q,∠CPQ=135°,求直线PQ的解析式.
如图,抛物线y=x2-3x+2与x轴交于A,B两点,与y轴交于点C,连接AC,将直线AC向右平移交抛物线于点P,交x轴于Q,∠CPQ=135°,求直线PQ的解析式.