题目内容
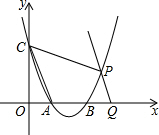 如图,抛物线y=x2-3x+2与x轴交于A,B两点,与y轴交于点C,连接AC,将直线AC向右平移交抛物线于点P,交x轴于Q,∠CPQ=135°,求直线PQ的解析式.
如图,抛物线y=x2-3x+2与x轴交于A,B两点,与y轴交于点C,连接AC,将直线AC向右平移交抛物线于点P,交x轴于Q,∠CPQ=135°,求直线PQ的解析式.考点:抛物线与x轴的交点
专题:计算题
分析:利用抛物线与x轴的交点问题得到A(1,0),B(2,0),易得C点坐标(0,2),再利用待定系数法确定直线AC的解析式为y=-2x+2;作AE⊥AC交直线CP于D,作DE⊥x轴于E,如图,根据平行线的性质由AC∥PQ得∠ACP=45°,则△ACD为等腰直角三角形,所以AC=AD,接着证明△ACO≌△DAE,得到AE=OC=2,DE=OA=1,于是可确定D点坐标为(3,1),再利用待定系数法求出直线CD的解析式为y=-
x+2,然后解方程组
得到P点坐标为(
,
),由于PQ∥AC,则直线PQ的解析式可设为y=-2x+t,然后把P(
,
)代入求出t即可得到直线PQ的解析式.
| 1 |
| 3 |
|
| 8 |
| 3 |
| 10 |
| 9 |
| 8 |
| 3 |
| 10 |
| 9 |
解答: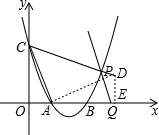 解:把y=0代入y=x2-3x+2得x2-3x+2=0,解得x1=1,x2=2,
解:把y=0代入y=x2-3x+2得x2-3x+2=0,解得x1=1,x2=2,
则A(1,0),B(2,0),
把x=0代入y=x2-3x+2得y=2,则C点坐标为(0,2),
设直线AC的解析式为y=kx+b,
把A(1,0)、C(0,2)代入得
,
解得
,
所以直线AC的解析式为y=-2x+2;
作AE⊥AC交直线CP于D,作DE⊥x轴于E,如图,
∵AC∥PQ,
∴∠ACP=180°-∠CPQ=180°-135°=45°,
∴△ACD为等腰直角三角形,
∴AC=AD,
∵∠CAO+∠DAE=90°,∠CAO+∠ACO=90°,
∴∠ACO=∠EAD,
在△ACO和△DAE中,
,
∴△ACO≌△DAE(AAS),
∴AE=OC=2,DE=OA=1,
∴D点坐标为(3,1),
设直线CD的解析式为y=mx+n,
把C(0,2)、D(3,1)代入得
,
解得
,
则直线CD的解析式为y=-
x+2,
解方程组
得
或
,
∴P点坐标为(
,
),
∵PQ∥AC,
∴直线PQ的解析式可设为y=-2x+t,
把P(
,
)代入得-2×
+t=
,
解得t=
,
∴直线PQ的解析式为y=-2x+
.
 解:把y=0代入y=x2-3x+2得x2-3x+2=0,解得x1=1,x2=2,
解:把y=0代入y=x2-3x+2得x2-3x+2=0,解得x1=1,x2=2,则A(1,0),B(2,0),
把x=0代入y=x2-3x+2得y=2,则C点坐标为(0,2),
设直线AC的解析式为y=kx+b,
把A(1,0)、C(0,2)代入得
|
解得
|
所以直线AC的解析式为y=-2x+2;
作AE⊥AC交直线CP于D,作DE⊥x轴于E,如图,
∵AC∥PQ,
∴∠ACP=180°-∠CPQ=180°-135°=45°,
∴△ACD为等腰直角三角形,
∴AC=AD,
∵∠CAO+∠DAE=90°,∠CAO+∠ACO=90°,
∴∠ACO=∠EAD,
在△ACO和△DAE中,
|
∴△ACO≌△DAE(AAS),
∴AE=OC=2,DE=OA=1,
∴D点坐标为(3,1),
设直线CD的解析式为y=mx+n,
把C(0,2)、D(3,1)代入得
|
解得
|
则直线CD的解析式为y=-
| 1 |
| 3 |
解方程组
|
|
|
∴P点坐标为(
| 8 |
| 3 |
| 10 |
| 9 |
∵PQ∥AC,
∴直线PQ的解析式可设为y=-2x+t,
把P(
| 8 |
| 3 |
| 10 |
| 9 |
| 8 |
| 3 |
| 10 |
| 9 |
解得t=
| 58 |
| 9 |
∴直线PQ的解析式为y=-2x+
| 58 |
| 9 |
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.也考查了利用待定系数法求一次函数解析式和利用方程组的解求两函数交点坐标.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
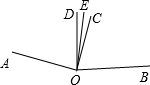 如图,已知∠AOB=165°,AO⊥OC,DO⊥OB,OE平分∠COD,求∠COE的度数.
如图,已知∠AOB=165°,AO⊥OC,DO⊥OB,OE平分∠COD,求∠COE的度数. 在一个大圆盘中有4个小圆盘,已知大小圆盘的直径都是整数,阴影部分的面积为7πcm2.求大小圆盘的半径是多少?
在一个大圆盘中有4个小圆盘,已知大小圆盘的直径都是整数,阴影部分的面积为7πcm2.求大小圆盘的半径是多少? 如图,△ABC中,点O是∠ABC、∠ACB角平分线的交点,AB+BC+AC=12,过O作OD⊥BC于D点,且OD=2,求△ABC的面积.
如图,△ABC中,点O是∠ABC、∠ACB角平分线的交点,AB+BC+AC=12,过O作OD⊥BC于D点,且OD=2,求△ABC的面积.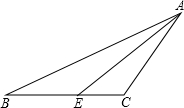 如图,在△ABC中,∠C-∠B=90°,AE是∠BAC的平分线,求∠AEC的度数.
如图,在△ABC中,∠C-∠B=90°,AE是∠BAC的平分线,求∠AEC的度数.