题目内容
18.已知抛物线$y=\frac{1}{2}{x^2}+bx$经过点A(2,0).设点C(3,-3),请在抛物线的对称轴上确定一点D,使得|AD-CD|的值最大,则D点的坐标为(1,3).分析 依照题意画出图形,连接AC交抛物线的对称轴于点D,根据三角形内两边之差小于第三边可得出此种作法得出的点D使得|AD-CD|的值最大,将点A的坐标代入抛物线解析式即可得出关于b的一元一次方程,解方程即可得出抛物线的解析式,由抛物线的解析式可得出抛物线的对称轴的解析式,由待定系数法求出直线AC的解析式,令x=1即可得出结论.
解答 解:依照题意画出图形,连接AC交抛物线的对称轴于点D,此时|AD-CD|的值最大,如图所示.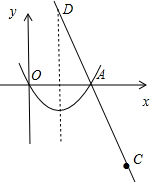
∵抛物线$y=\frac{1}{2}{x^2}+bx$经过点A(2,0),
∴有0=2+2b,解得:b=-1.
∴抛物线的解析式为y=$\frac{1}{2}{x}^{2}$-x,
∴抛物线的对称轴为x=-$\frac{-1}{2×\frac{1}{2}}$=1.
设直线AC的解析式为y=kx+b(k≠0),
∴$\left\{\begin{array}{l}{0=2k+b}\\{-3=3k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-3}\\{b=6}\end{array}\right.$,
∴直线AC的解析式为y=-3x+6.
令x=1,则y=-3+6=3.
即点D的坐标为(1,3).
故答案为:(1,3).
点评 本题考查了二次函数的性质、待定系数法求函数解析式以及三角形的三边关系,根据三角形的三边关系确定点D的位置是解题的关键.

练习册系列答案
相关题目
3. 如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )
如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )
 如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )
如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )| A. | 12cm | B. | 10cm | C. | 8cm | D. | 6cm |
10.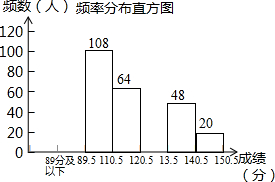 某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:
某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:
频率分布表
请你根据不完整的频率分布表,解答下列问题:
(1)补全频率分布表;
(2)补全频数分布直方图;
(3)若将得分转化为等级,规定得分“89分及以下”分评为“D”,“89.5-110.5分”评为“C”,“110.5-130.5扥”评为“B”,“130.5-150.5分”评为“A”,这次15000名学生中约有多少人评为“D”?如果随机抽取一名学生的成绩等级,则这名学生的成绩评为“A”、“B”、“C”、“D”哪一个等级的可能性大?请说明理由.
 某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:
某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:频率分布表
| 分组 | 频数 | 频率 |
| 89分及以下 | ||
| 89.5-110.5 | 108 | |
| 110.5-120.5 | 64 | 0.16 |
| 120.5-130.5 | 0.20 | |
| 130.5-140.5 | 48 | |
| 140.5-150.5 | 20 | 0.05 |
| 合计 | 400 | 1 |
(1)补全频率分布表;
(2)补全频数分布直方图;
(3)若将得分转化为等级,规定得分“89分及以下”分评为“D”,“89.5-110.5分”评为“C”,“110.5-130.5扥”评为“B”,“130.5-150.5分”评为“A”,这次15000名学生中约有多少人评为“D”?如果随机抽取一名学生的成绩等级,则这名学生的成绩评为“A”、“B”、“C”、“D”哪一个等级的可能性大?请说明理由.
 如图,当具备什么条件时,AB∥EF?请说明理由(写出一个即可)
如图,当具备什么条件时,AB∥EF?请说明理由(写出一个即可)
 直线MN表示一条河流的河岸,在河流同旁有A、B两个村庄,现要在河边修建一个供水站给A、B供水.问:这个供水站建在什么地方,可以使铺设管道最短?请在图中找出表示供水站的点P.
直线MN表示一条河流的河岸,在河流同旁有A、B两个村庄,现要在河边修建一个供水站给A、B供水.问:这个供水站建在什么地方,可以使铺设管道最短?请在图中找出表示供水站的点P.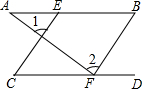 如图,已知∠1=∠2,∠B=∠C,试说明AB∥CD.
如图,已知∠1=∠2,∠B=∠C,试说明AB∥CD.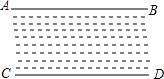 如图所示,直线AB,CD表示一条小河的两条河岸线,小明和小刚想利用数学知识判断这里两条河岸线是否平行,两人现在分别在小河的两侧,每人手中各有两根标杆和一个测角仪,请你帮他们想象办法.
如图所示,直线AB,CD表示一条小河的两条河岸线,小明和小刚想利用数学知识判断这里两条河岸线是否平行,两人现在分别在小河的两侧,每人手中各有两根标杆和一个测角仪,请你帮他们想象办法.