题目内容
6．若$\sqrt{a-2}$+|b+$\sqrt{5}$|=0，则|a+b|=$\sqrt{5}$-2．分析 首先依据非负数的性质可求得a、b的值，然后依据绝对值的性质化简即可．
解答 解：∵$\sqrt{a-2}$+|b+$\sqrt{5}$|=0，
∴a=2，b=-$\sqrt{5}$．
∴a+b=2-$\sqrt{5}$＜0，
∴|a+b|=-（2-$\sqrt{5}$）=$\sqrt{5}$-2．
故答案为：$\sqrt{5}$-2．
点评 本题主要考查的是非负数的性质、绝对值的性质，依据非负数的性质求得a、b的值是解题的关键．
练习册系列答案
相关题目
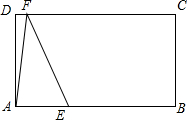在矩形ABCD中，AB=6，AD=2$\sqrt{3}$，E是AB边上一点，AE=2，F是直线CD上一动点，将△AEF沿直线EF折叠，点A的对应点为点A′，当点E、A′、C三点在一条直线上时，DF的长度为6+2$\sqrt{7}$或6-2$\sqrt{7}$．
如图，△ABC中，AB=BC，以AB为直径的⊙O交AC于点D，且CD=BD．
1．如图，∠1和∠2是对顶角的是（ ）
| A． |  | B． |  | C． |  | D． |  |
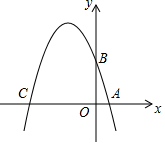如图，在平面直角坐标系xOy中，A、B、C三点分别为坐标轴上的三个点，且OA=1，OB=3，OC=4．
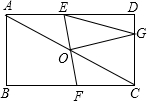如图，矩形ABCD中，对角线AC的中点为O，过O作直线EF交AD于E，交BC于F．