题目内容
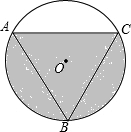 如图,若⊙O的内接正△ABC的边长为12cm,求图中阴影部分的面积.
如图,若⊙O的内接正△ABC的边长为12cm,求图中阴影部分的面积.考点:扇形面积的计算,等边三角形的性质
专题:
分析:利用正三角形的性质得出∠AOC的度数以及DO,CO的长,进而得出答案.
解答: 解:连接AO,CO,过点O作OD⊥AC于点D,
解:连接AO,CO,过点O作OD⊥AC于点D,
∵⊙O的内接正△ABC的边长为12cm,OD⊥AC,AO=CO,
∴DC=AD=6cm,∠AOC=120°,∠DOC=60°,
故tan60°=
,
解得:DO=2
(cm),
故CO=4
cm,
图中阴影部分的面积为:
+
×DO×AC=32π+
×2
×12=(32π+12
)cm2.
 解:连接AO,CO,过点O作OD⊥AC于点D,
解:连接AO,CO,过点O作OD⊥AC于点D,∵⊙O的内接正△ABC的边长为12cm,OD⊥AC,AO=CO,
∴DC=AD=6cm,∠AOC=120°,∠DOC=60°,
故tan60°=
| 6 |
| DO |
解得:DO=2
| 3 |
故CO=4
| 3 |
图中阴影部分的面积为:
240π×(4
| ||
| 360 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:此题主要考查了扇形面积以及等边三角形的性质等知识,得出OD的长是解题关键.

练习册系列答案
相关题目
若代数式2x2+3x+7的值是8,则代数式9-4x2-6x的值是( )
| A、2 | B、-17 | C、-7 | D、7 |
 如图所示,是一块在电脑屏幕上出现的矩形色块图,由6个不同颜色的正方形组成,已知中间最小的一个正方形的边长为1,那么这个长方形色块图的面积为
如图所示,是一块在电脑屏幕上出现的矩形色块图,由6个不同颜色的正方形组成,已知中间最小的一个正方形的边长为1,那么这个长方形色块图的面积为
 如图,已知过A、C、D三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=57°,那么∠ABC=
如图,已知过A、C、D三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=57°,那么∠ABC= 如图,在直角三角形ABC中,∠ACB=90°,AC=AE,BC=BF,则∠ECF=
如图,在直角三角形ABC中,∠ACB=90°,AC=AE,BC=BF,则∠ECF=