题目内容
在一个不透明的纸箱里装有红、黄两种颜色的小球,它们除颜色外完全相同,其中红球有3个,黄球有1个. 现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的一方得电影票).游戏规则是:由小明与小亮同时从纸箱里随机摸出1个球.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由.
考点:游戏公平性,列表法与树状图法
专题:
分析:游戏是否公平,关键要看游戏双方获胜的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.
解答:解:如图所示:

由上述树状图知:所有可能出现的结果共有12种.
P(小明赢)=
=
,P(小亮赢)=
.
故此游戏对双方公平.

由上述树状图知:所有可能出现的结果共有12种.
P(小明赢)=
| 6 |
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
故此游戏对双方公平.
点评:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
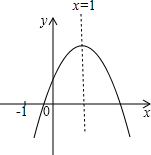 已知二次函数y=ax2+bx+c的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②a+c>b;③4a+2b+c>0;④2a+b=0;⑤b2-4ac>0
其中正确的结论有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
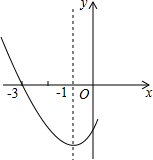 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=-1,且过点(-3,0),下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=-1,且过点(-3,0),下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(| 5 |
| 2 |
| A、①② | B、②③ |
| C、①②④ | D、②③④ |
如图,甲、乙、丙三个三角形中和△ABC全等的图形有( )


| A、甲 | B、乙 | C、丙 | D、乙和丙 |
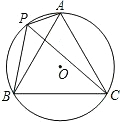 如图,A、P、B、C是⊙O上四点,且∠APC=∠CPB=60?.连接CP、BP、AP,
如图,A、P、B、C是⊙O上四点,且∠APC=∠CPB=60?.连接CP、BP、AP,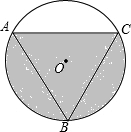 如图,若⊙O的内接正△ABC的边长为12cm,求图中阴影部分的面积.
如图,若⊙O的内接正△ABC的边长为12cm,求图中阴影部分的面积.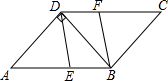 如图,在平行四边形ABCD中,∠A=60°,AD=6,且AD⊥BD,点E,F分别是边AB,CD上的动点,且AE=CF.
如图,在平行四边形ABCD中,∠A=60°,AD=6,且AD⊥BD,点E,F分别是边AB,CD上的动点,且AE=CF.