题目内容
有这样的一个定理:夹在两条平行线间的平行线段相等.下面经历探索与应用的过程.
探索:
已知:如图1,AD∥BC,AB∥CD.求证:AB=CD.
应用此定理进行证明求解.
应用一、已知:如图2,AD∥BC,AD<BC,AB=CD.求证:∠B=∠C;

应用二、已知:如图3,AD∥BC,AC⊥BD,AC=4,BD=3.求:AD与BC两条线段的和.
探索:
已知:如图1,AD∥BC,AB∥CD.求证:AB=CD.
应用此定理进行证明求解.
应用一、已知:如图2,AD∥BC,AD<BC,AB=CD.求证:∠B=∠C;

应用二、已知:如图3,AD∥BC,AC⊥BD,AC=4,BD=3.求:AD与BC两条线段的和.
考点:平行线之间的距离,全等三角形的判定与性质
专题:
分析:探索:利用平行线的性质得出,∠DAC=∠BCA,∠BAC=∠DCA,进而得出△ABC≌△CDA(ASA),求出即可;
应用一:作DE∥AB交BC于点E,利用平行线的性质得出∠B=∠C;
应用二:利用平行线的性质结合勾股定理得出AD与BC两条线段的和.
应用一:作DE∥AB交BC于点E,利用平行线的性质得出∠B=∠C;
应用二:利用平行线的性质结合勾股定理得出AD与BC两条线段的和.
解答: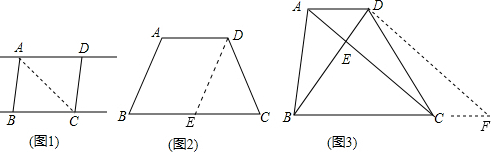 探索:
探索:
证明:如图1,
连接AC,
∵AD∥BC,∴∠DAC=∠BCA
∵AB∥CD.∴∠BAC=∠DCA
在△ABC和△CDA中,
,
∴△ABC≌△CDA(ASA),
∴AB=CD;
应用一:
证明:如图2,
作DE∥AB交BC于点E,
∵AD∥BC,
∴AB=DE
∵AB=CD,
∴DE=CD,
∴∠DEC=∠C
∵DE∥AB,
∴∠B=∠DEC,
∴∠B=∠C;
应用二、
解:如图3,
作DE∥AC交BC的延长线于点F
∵AD∥BC,∴AC=DF、AD=CF,
∵DE∥AC,∴∠BDF=∠BEC,
∵AC⊥BD,∴∠BDF=∠BEC=90°,
在Rt△BDF中,由勾股定理得:BF=5,
故BC+AD=BC+CF=BF=5.
 探索:
探索:证明:如图1,
连接AC,
∵AD∥BC,∴∠DAC=∠BCA
∵AB∥CD.∴∠BAC=∠DCA
在△ABC和△CDA中,
|
∴△ABC≌△CDA(ASA),
∴AB=CD;
应用一:
证明:如图2,
作DE∥AB交BC于点E,
∵AD∥BC,
∴AB=DE
∵AB=CD,
∴DE=CD,
∴∠DEC=∠C
∵DE∥AB,
∴∠B=∠DEC,
∴∠B=∠C;
应用二、
解:如图3,
作DE∥AC交BC的延长线于点F
∵AD∥BC,∴AC=DF、AD=CF,
∵DE∥AC,∴∠BDF=∠BEC,
∵AC⊥BD,∴∠BDF=∠BEC=90°,
在Rt△BDF中,由勾股定理得:BF=5,
故BC+AD=BC+CF=BF=5.
点评:此题主要考查了勾股定理以及全等三角形的判定与性质和平行线的性质等知识,正确作出辅助线是解题关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
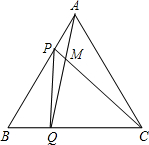 如图,点P、Q是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A出发,沿线段AB运动,点Q从顶点B出发,沿线段BC运动,且它们的速度都为1cm/s,连接AQ、CP交于点M,在P、Q运动的过程中,假设运动时间为t秒,则当t=
如图,点P、Q是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A出发,沿线段AB运动,点Q从顶点B出发,沿线段BC运动,且它们的速度都为1cm/s,连接AQ、CP交于点M,在P、Q运动的过程中,假设运动时间为t秒,则当t=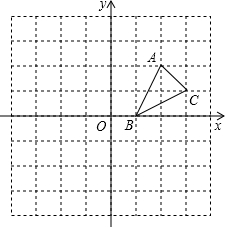 如图,方格纸中的每个小方格都是边长为1个单位的正方形,建立如图所示的平面直角坐标系,△ABC的顶点均在格点上,点B的坐标为(1,0)
如图,方格纸中的每个小方格都是边长为1个单位的正方形,建立如图所示的平面直角坐标系,△ABC的顶点均在格点上,点B的坐标为(1,0)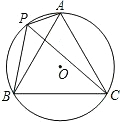 如图,A、P、B、C是⊙O上四点,且∠APC=∠CPB=60?.连接CP、BP、AP,
如图,A、P、B、C是⊙O上四点,且∠APC=∠CPB=60?.连接CP、BP、AP, 已知如图,△ABC中,AD为BC的中线,E为AD的中点,延长CE交AB于点F,求
已知如图,△ABC中,AD为BC的中线,E为AD的中点,延长CE交AB于点F,求 如图,若⊙O的内接正△ABC的边长为12cm,求图中阴影部分的面积.
如图,若⊙O的内接正△ABC的边长为12cm,求图中阴影部分的面积.