题目内容
 如图,在直角三角形ABC中,∠ACB=90°,AC=AE,BC=BF,则∠ECF=
如图,在直角三角形ABC中,∠ACB=90°,AC=AE,BC=BF,则∠ECF=考点:等腰三角形的性质
专题:
分析:根据等腰三角形的性质得:∠AEC=∠ACE=
,∠BFC=∠BCF=
,从而利用∠EFC=∠BCF+∠ACE-∠ACB=
+
-90°=45°求解.
| 180°-∠A |
| 2 |
| 180°-∠B |
| 2 |
| 180°-∠A |
| 2 |
| 180°-∠B |
| 2 |
解答:解:∵AE=AC,BC=BF,
∴∠AEC=∠ACE=
,∠BFC=∠BCF=
,
∴∠ECF=∠BCF+∠ACE-∠ACB=
+
-90°=45°,
故答案为:45.
∴∠AEC=∠ACE=
| 180°-∠A |
| 2 |
| 180°-∠B |
| 2 |
∴∠ECF=∠BCF+∠ACE-∠ACB=
| 180°-∠A |
| 2 |
| 180°-∠B |
| 2 |
故答案为:45.
点评:本题考查了等腰三角形的性质中的等边对等角,难度较小,解题的关键是发现要求的角和直角之间的关系.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
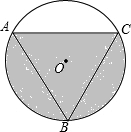 如图,若⊙O的内接正△ABC的边长为12cm,求图中阴影部分的面积.
如图,若⊙O的内接正△ABC的边长为12cm,求图中阴影部分的面积.