题目内容
 如图,已知过A、C、D三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=57°,那么∠ABC=
如图,已知过A、C、D三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=57°,那么∠ABC=考点:圆周角定理
专题:计算题
分析:连接EC、ED,如图,设∠B=x,根据等腰三角形的性质由EA=EC得∠A=∠ACE,再根据三角形内角和定理得到∠4=180°-2∠A=66°,而DB=DE,则∠1=∠B=x,利用三角形外角性质得∠2=∠1+∠B=2x,再利用EC=ED得到∠3=∠2=2x,然后根据三角形外角性质得到2x+x=66°,即得x=22°.
解答:解:连接EC、ED,如图,设∠B=x,
∵EA=EC,
∴∠A=∠ACE,
∴∠4=180°-2∠A=180°-2×57°=66°,
∵DB=DE,
∴∠1=∠B=x,
∴∠2=∠1+∠B=2x,
而EC=ED,
∴∠3=∠2=2x,
∵∠4=∠3+∠B,
∴2x+x=66°,即得x=22°,
即∠ABC=22°.
故答案为22.

∵EA=EC,
∴∠A=∠ACE,
∴∠4=180°-2∠A=180°-2×57°=66°,
∵DB=DE,
∴∠1=∠B=x,
∴∠2=∠1+∠B=2x,
而EC=ED,
∴∠3=∠2=2x,
∵∠4=∠3+∠B,
∴2x+x=66°,即得x=22°,
即∠ABC=22°.
故答案为22.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
 如图,BD是∠ABC平分线,DE⊥AB于E,AB=36cm,BC=24cm,S△ABC=144cm2,DE长是( )
如图,BD是∠ABC平分线,DE⊥AB于E,AB=36cm,BC=24cm,S△ABC=144cm2,DE长是( )| A、4.6cm | B、4.8cm |
| C、5cm | D、无法确定 |
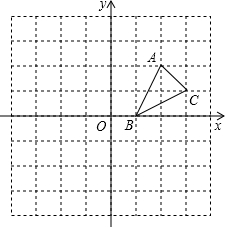 如图,方格纸中的每个小方格都是边长为1个单位的正方形,建立如图所示的平面直角坐标系,△ABC的顶点均在格点上,点B的坐标为(1,0)
如图,方格纸中的每个小方格都是边长为1个单位的正方形,建立如图所示的平面直角坐标系,△ABC的顶点均在格点上,点B的坐标为(1,0) 已知如图,△ABC中,AD为BC的中线,E为AD的中点,延长CE交AB于点F,求
已知如图,△ABC中,AD为BC的中线,E为AD的中点,延长CE交AB于点F,求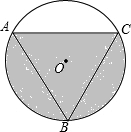 如图,若⊙O的内接正△ABC的边长为12cm,求图中阴影部分的面积.
如图,若⊙O的内接正△ABC的边长为12cm,求图中阴影部分的面积.