Question

如图，过y轴上任意一点P，作x轴的平行线，分别与反比例函数y₁和y2=

2

x

的图形交于点A和点B，若点C为x轴上的任意一点，连接AC、BC，若S_△ABC=8，则y₁的解析式为

 

．

Answer 1

考点：反比例函数系数k的几何意义

专题：计算题

分析：设y₁的解析式为y=

k

x

，连接OA、OB，如图，由于AB∥x轴，根据三角形面积公式得到S_△OAB=S_△ABC=8，根据反比例函数k的几何意义得到S_△OBP=1，
则S_△OAP=7，再根据反比例函数k的几何意义得S_△OAP=

1

2

|k|=7，解得k=-14，然后写出反比例函数解析式．

解答：解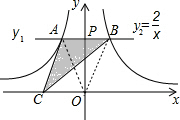：设y₁的解析式为y=

k

x

，
连接OA、OB，如图，
∵AB∥x轴，
∴S_△OAB=S_△ABC=8，S_△OBP=

1

2

×|2|=1，
∴S_△OAP=8-1=7，
∵S_△OAP=

1

2

|k|，
∴

1

2

|k|=7，
而k＜0，
∴k=-14，
∴y₁的解析式为y=-

14

x

．
故答案为y=-

14

x

．

点评：本题考查了反比例函数y=

k

x

（k≠0）系数k的几何意义：从反比例函数y=

k

x

（k≠0）图象上任意一点向x轴和y轴作垂线，垂线与坐标轴所围成的矩形面积为|k|．