题目内容
15.下列分式中最简分式为( )| A. | $\frac{4}{2x}$ | B. | $\frac{2x}{{x}^{2}+1}$ | C. | $\frac{x-1}{{x}^{2}-1}$ | D. | $\frac{1-x}{x-1}$ |
分析 最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.
解答 解:A、$\frac{4}{2x}=\frac{2}{x}$可以约分,错误;
B、$\frac{2x}{{x}^{2}+1}$是最简分式,正确;
C、$\frac{x-1}{{x}^{2}-1}=\frac{1}{x+1}$可以约分,错误;
D、$\frac{1-x}{x-1}=-1$可以约分,错误;
故选:B
点评 本题所要考查的知识点是最简分式的概念.判断一个分式是否是最简分式,关键是看它的分子与分母之间是否存在公因式.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
5.要使二次根式$\sqrt{3-m}$有意义,则m的取值范围为( )
| A. | m<3 | B. | m≤3 | C. | m>3 | D. | m≥3 |
6.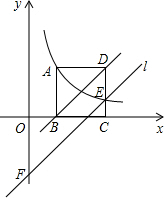 如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )
如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )
 如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )
如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )| A. | (0,-$\frac{7}{3}$) | B. | (0,-$\frac{8}{3}$) | C. | (0,-3) | D. | (0,-$\frac{10}{3}$) |
3.已知,点A(-6,y1)和点B(1,y2)都在直线y=-$\frac{1}{2}$x-1上,那么y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不确定 |
20.若关于x的分式方程$\frac{2}{x-2}$+$\frac{mx}{{x}^{2}-4}$=$\frac{3}{x+2}$有增根,则m的值是( )
| A. | 1 | B. | -4或6 | C. | 6或1 | D. | 1或-4或6 |
 如图,已知:等边△ABC边长为4cm,AD⊥BC于点D,求△ABC的面积.
如图,已知:等边△ABC边长为4cm,AD⊥BC于点D,求△ABC的面积.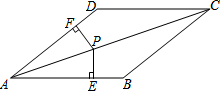 如图,在四边形ABCD中,AB∥CD,∠B=∠D.
如图,在四边形ABCD中,AB∥CD,∠B=∠D. 如图,边长为4的正方形ABCD中对角线AC、BD相交于点O,OE⊥CD,则OE=2.
如图,边长为4的正方形ABCD中对角线AC、BD相交于点O,OE⊥CD,则OE=2.