题目内容
10．解不等式组：$\left\{\begin{array}{l}{3x+45＞-1}\\{3x+45≤2}\end{array}\right.$．分析 分别求出两个不等式的解集，求其公共解．
解答 解：$\left\{\begin{array}{l}{3x+45＞-1①}\\{3x+45≤2②}\end{array}\right.$，
解不等式①得：x＞-$\frac{46}{3}$，
解不等式②得：x≤-$\frac{43}{3}$，
所以不等式组的解集是$-\frac{46}{3}＜x≤-\frac{43}{3}$
点评 此题考查不等式组的解法，求不等式组的公共解，要遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．要注意应用数形结合．
练习册系列答案
相关题目
20．
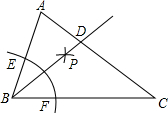如图，已知△ABC，∠ABC=2∠C，以B为圆心任意长为半径作弧，交BA、BC于点E、F，分别以E、F为圆心，以大于$\frac{1}{2}$EF的长为半径作弧，两弧交于点P，作射线BP交AC于点，则下列说法不正确的是（ ）
如图，已知△ABC，∠ABC=2∠C，以B为圆心任意长为半径作弧，交BA、BC于点E、F，分别以E、F为圆心，以大于$\frac{1}{2}$EF的长为半径作弧，两弧交于点P，作射线BP交AC于点，则下列说法不正确的是（ ）| A． | ∠ADB=∠ABC | B． | AB=BD | C． | AC=AD+BD | D． | ∠ABD=∠BCD |
如图，小虎站在自己家的A处，测得某信号塔CD的顶点C的俯角∠EAC为37°，底部D点的俯角∠EAD为50°，已知小虎家距地面的高度AB为60m．