题目内容
20.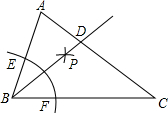 如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E、F,分别以E、F为圆心,以大于$\frac{1}{2}$EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )
如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E、F,分别以E、F为圆心,以大于$\frac{1}{2}$EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )| A. | ∠ADB=∠ABC | B. | AB=BD | C. | AC=AD+BD | D. | ∠ABD=∠BCD |
分析 根据作图方法可得BD平分∠ABC,进而可得∠ABD=∠DBC=$\frac{1}{2}$∠ABC,然后根据条件∠ABC=2∠C可证明∠ABD=∠DBC=∠C,再根据三角形内角和外角的关系可得A说法正确;根据等角对等边可得DB=CD,进而可得AC=AD+BD,可得C说法正确;根据等量代换可得D正确.
解答 解:由题意可得BD平分∠ABC,
A、∵BD平分∠ABC,
∴∠ABD=∠DBC=$\frac{1}{2}$∠ABC,
∵∠ABC=2∠C,∠ADB=∠C+∠DBC,
∴∠ADB=2∠C,
∴∠ADB=∠ABC,故A不合题意;
B、∵∠A≠∠ADB,
∴AB≠BD,故此选项符合题意;
C、∵∠DBC=$\frac{1}{2}$∠ABC,∠ABC=2∠C,
∴∠DBC=∠C,
∴DC=BD,
∵AC=AD+DC,
∴AC=AD+BD,故此选项不合题意;
D、∵∠ABD=$\frac{1}{2}$∠ABC,∠ABC=2∠C,
∴∠ABD=∠C,故此选项不合题意;
故选:B.
点评 此题主要考查了基本作图,以及等腰三角形的判定和性质,关键是掌握角平分线的作法.

练习册系列答案
相关题目
10.一只不透明的袋子中装有1个白球,2个黄球和3个红球,每个球除颜色外都相同,将球搅匀,从中任意摸出一个球.如果想使摸到这三种颜色的球的概率相等,下列做法正确的是( )
| A. | 向袋子里分别投放1个白球,1个黄球,1个红球 | |
| B. | 向袋子里分别投放3个白球,2个黄球,1个红球 | |
| C. | 向袋子里分别投放2个白球,1个红球 | |
| D. | 向袋子里投放2个白球 |
11. 如图是函数y=$\frac{a}{x}$-1的图象,则关于x的分式方程$\frac{a}{x}$=3的解是( )
如图是函数y=$\frac{a}{x}$-1的图象,则关于x的分式方程$\frac{a}{x}$=3的解是( )
 如图是函数y=$\frac{a}{x}$-1的图象,则关于x的分式方程$\frac{a}{x}$=3的解是( )
如图是函数y=$\frac{a}{x}$-1的图象,则关于x的分式方程$\frac{a}{x}$=3的解是( )| A. | x=6 | B. | x=0.5 | C. | x=2 | D. | x=1 |
15.下列运算正确的是( )
| A. | 3a2-a2=2 | B. | a+a2=a3 | C. | (-2a)3=-8a3 | D. | a6÷a2=a3 |
9. 如图,点A、B、C在圆O上,∠A=60°,则∠BOC=( )
如图,点A、B、C在圆O上,∠A=60°,则∠BOC=( )
 如图,点A、B、C在圆O上,∠A=60°,则∠BOC=( )
如图,点A、B、C在圆O上,∠A=60°,则∠BOC=( )| A. | 60° | B. | 90° | C. | 120° | D. | 135° |