题目内容
4.解不等式组$\left\{\begin{array}{l}{\frac{x+2}{3}<1}\\{2(1-x)≤4}\end{array}\right.$把解集在数轴上表示出来,并写出解集中的整数解.
分析 先求出每一个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{\frac{x+2}{3}<1①}\\{2(1-x)≤4②}\end{array}\right.$
∵解不等式①得:x<1,
解不等式②得:x≥-1,
∴不等式组的解集为-1≤x<1,
在数轴上表示不等式组的解集为: ,
,
不等式组的整数解为-1,0.
点评 本题考查了解一元一次不等式组,在数轴上表示不等式组的解集,不等式组的整数解的应用,能根据不等式的解集找出不等式组的解集是解此题的关键.

练习册系列答案
相关题目
14.对于图形的旋转,下列说法不正确的是( )
| A. | 对应点到旋转中心的距离相等 | B. | 图形上每一部分旋转的角度相同 | ||
| C. | 旋转前后的两个图形全等 | D. | 图形上每一点所经过的路程相同 |
12.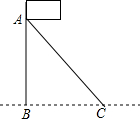 如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )
如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )
 如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )
如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )| A. | 6sin50° | B. | 6cos50° | C. | $\frac{6}{sin50°}$ | D. | $\frac{6}{cos50°}$ |
19.一名射击爱好者5次射击的中靶环数如下:6,7,9,8,9,这五个数据的众数和中位数分别是( )
| A. | 9,8 | B. | 9,7 | C. | 8,9 | D. | 9,9 |
9.下列计算正确的是( )
| A. | 2a5+a5=3a10 | B. | a2•a3=a6 | C. | (a2)3=a5 | D. | a10÷a2=a8 |
16.下列运算正确的是( )
| A. | a3•a2=a6 | B. | (a2)2=a4 | C. | (-3a)3=-9a3 | D. | a4+a5=a9 |
13.下列不是分解因式的是( )
| A. | 10a2b+6ab2=2ab(5a+3b) | B. | (2x+y)(x-y)=2x2-xy-y2 | ||
| C. | y2-9z2=(y+3z)(y-3z) | D. | m2n2-2mna+a2=(mn-a)2 |