题目内容
3.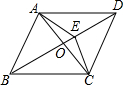 如图,在菱形ABCD中,∠ABC=70°,AC与BD相交于点O,E是OD上一点,若有AE=DE,则下列说法不正确的是( )
如图,在菱形ABCD中,∠ABC=70°,AC与BD相交于点O,E是OD上一点,若有AE=DE,则下列说法不正确的是( )| A. | 点E是△ACD的内心 | B. | ∠DBC=35° | C. | CE=DE | D. | △ABO≌△CBO |
分析 由已知条件和菱形的性质易求∠DBC的度数以及CE=DE,由全等三角形的判断方法可证明△ABO≌△CBO,进而可得问题的选项.
解答 解:∵四边形ABCD是菱形,
∴∠ABD=∠DBC=$\frac{1}{2}∠ABC$,AB=BC,AO=CO,
∴∠DBC=35°,故选项B正确;
在△ABO和△CBO中
$\left\{\begin{array}{l}{AB=CB}\\{∠ABC=∠CBD}\\{AO=CO}\end{array}\right.$,
∴△ABO≌△CBO(SAS)故选项D正确;
∵AC⊥BD,AO=CO,
∴AE=CE,
∵AE=DE,
∴CE=DE,故选项C正确,
故选A.
点评 本题考查了菱形的性质、全等三角形的判定和性质以及垂直平分线的性质,熟记菱形的各种性质是解题关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
18.若a<b,则下列不等式的变形中不正确的是( )
| A. | a+5<b+5 | B. | $\frac{a}{5}$$<\frac{b}{5}$ | C. | 5a-1<5b-1 | D. | 5-a<5-b |
15.下列命题是真命题的是( )
| A. | 两条不相交的直线就是平行线 | |
| B. | 过任意一点可以作已知直线的一条平行线 | |
| C. | 过直线外任意一点作已知直线的垂线,可以作无数条 | |
| D. | 直线外一点与直线上各点所连接的所有线段中,垂线段最短 |
12.已知直角三角形两边的长分别为5、12,则第三边的长为( )
| A. | 13 | B. | 60 | C. | 17 | D. | 13或$\sqrt{119}$ |
13.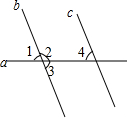 如图,已知直线b,c被直线a所截,∠1=65°,若要判断b∥c,则下列所给条件正确的是( )
如图,已知直线b,c被直线a所截,∠1=65°,若要判断b∥c,则下列所给条件正确的是( )
 如图,已知直线b,c被直线a所截,∠1=65°,若要判断b∥c,则下列所给条件正确的是( )
如图,已知直线b,c被直线a所截,∠1=65°,若要判断b∥c,则下列所给条件正确的是( )| A. | ∠2=115° | B. | ∠3=65° | C. | ∠4=65° | D. | ∠4=115° |
 数学活动课上,老师组织各学习小组同学动手操作,大胆猜想并加以验证.
数学活动课上,老师组织各学习小组同学动手操作,大胆猜想并加以验证.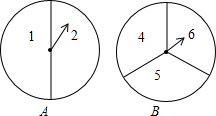 如图,有两个可以自由转动的均匀转盘A、B,分别被分成2等份和3等份,每份内均都有数字.小明和小亮用这两个转盘做游戏,游戏规则如下:分别转动转盘A和B,两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止),若和为偶数,则小明获胜;如果和为奇数,那么小亮获胜.
如图,有两个可以自由转动的均匀转盘A、B,分别被分成2等份和3等份,每份内均都有数字.小明和小亮用这两个转盘做游戏,游戏规则如下:分别转动转盘A和B,两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止),若和为偶数,则小明获胜;如果和为奇数,那么小亮获胜.