题目内容
16.在平面直角坐标系xOy中,已知点A(-3,-4),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是(4,-3).分析 先构建Rt△OAB,再把△OAB绕坐标原点O逆时针旋转90°得到△OA′B′,根据旋转的性质得到A′B′=AB=3,OB′=OB=4,∠OB′A′=∠OBA=90°,然后写出A′点的坐标.
解答 解:如图,
把△OAB绕坐标原点O逆时针旋转90°得到△OA′B′,则A′B′=AB=3,OB′=OB=4,∠OB′A′=∠OBA=90°,
所以点A′的坐标为(4,-3).
故答案为(4,-3).
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.通过把线段旋转的问题转化为直角三角形的性质解决问题.

练习册系列答案
相关题目
11.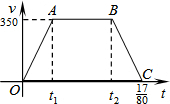 京沪高速铁路已开工建设,某校研究性学习以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C($\frac{17}{80}$,0),四边形OABC的面积为70,则t1-t2=( )
京沪高速铁路已开工建设,某校研究性学习以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C($\frac{17}{80}$,0),四边形OABC的面积为70,则t1-t2=( )
 京沪高速铁路已开工建设,某校研究性学习以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C($\frac{17}{80}$,0),四边形OABC的面积为70,则t1-t2=( )
京沪高速铁路已开工建设,某校研究性学习以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C($\frac{17}{80}$,0),四边形OABC的面积为70,则t1-t2=( )| A. | $\frac{1}{5}$ | B. | $\frac{3}{16}$ | C. | $\frac{7}{80}$ | D. | $\frac{31}{160}$ |
1.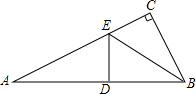 如图,在△ABC中,∠C=90°,沿过点B的一条直线BE,折叠△ABC,使点C恰好落在AB边的中点D处,则∠A的度数是( )
如图,在△ABC中,∠C=90°,沿过点B的一条直线BE,折叠△ABC,使点C恰好落在AB边的中点D处,则∠A的度数是( )
 如图,在△ABC中,∠C=90°,沿过点B的一条直线BE,折叠△ABC,使点C恰好落在AB边的中点D处,则∠A的度数是( )
如图,在△ABC中,∠C=90°,沿过点B的一条直线BE,折叠△ABC,使点C恰好落在AB边的中点D处,则∠A的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 45° |
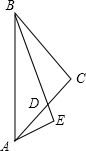 如图,△ABC中,BC=AC,∠ACB=90°,BD平分∠ABC,AE⊥BD,交BD延长线于E,
如图,△ABC中,BC=AC,∠ACB=90°,BD平分∠ABC,AE⊥BD,交BD延长线于E,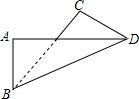 如图表示长方形纸片ABCD沿对角线BD折叠后的情况,图中有没有关于某条直线对称的图形?如有,请作出对称轴,有没有相等的线段、相等的角(不含直角)?如有,请写出相等的线段、相等的角.
如图表示长方形纸片ABCD沿对角线BD折叠后的情况,图中有没有关于某条直线对称的图形?如有,请作出对称轴,有没有相等的线段、相等的角(不含直角)?如有,请写出相等的线段、相等的角. 如图,矩形纸片ABCD中,AB=4cm,BC=8cm,现将A、C重合,使纸片折叠压平,设折痕为EF,
如图,矩形纸片ABCD中,AB=4cm,BC=8cm,现将A、C重合,使纸片折叠压平,设折痕为EF,