题目内容
6.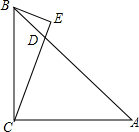 如图,等腰Rt△ABC中,∠ACB=90°,CA=CB,点D在AB上,AD=AC,BE⊥直线CD于E
如图,等腰Rt△ABC中,∠ACB=90°,CA=CB,点D在AB上,AD=AC,BE⊥直线CD于E(1)求∠BCD的度数;
(2)求证:CD=2BE;
(3)若点O是AB的中点,请直接写出三条线段CB、BD、CO之间的数量关系.
分析 (1)根据等腰直角三角形的性质得出∠A=45°,利用等腰三角形进行解答即可;
(2)作AH⊥CD于H,根据全等三角形的判定和性质解答即可;
(3)过D作DH⊥BC于点H,利用等腰直角三角形的性质证得Rt△COD≌Rt△CHD,得出CH=CO,进一步利用性质求得BC=CH+BH=CO+$\frac{\sqrt{2}}{2}$BD即可.
解答 解:(1)∵等腰Rt△ABC中,∠ACB=90°,CA=CB,
∴∠A=∠CBA=45°,
∵AD=AC,
∴∠ACD=67.5°,
∴∠BCD=90°-∠ACD=22.5°;
(2)作AH⊥CD于H,如图: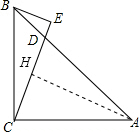
∵BE⊥直线CD于E,AC=AD,
∴CD=2CH,∠BEC=∠AHC=90°,
∵∠BCE+∠DCA=∠HAC+∠DCA=90°,
∴∠BCE=∠CAH,
在△CBE与△ACH中,
$\left\{\begin{array}{l}{∠BCE=∠CAH}\\{∠BEC=∠AHC=90°}\\{BC=AC}\end{array}\right.$,
∴△CBE≌△ACH(AAS),
∴CH=BE,
即CD=2CH=2BE;
(3)如图,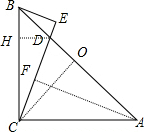
过D作DH⊥BC于点H,
由(1)可知∠BCD=22.5°,
∵O是AB的中点,
∴∠BCO=45°,
∴∠DCO=∠HCD=22.5°,
∴DO=DH,
在Rt△COD和Rt△CHD中,
$\left\{\begin{array}{l}{DO=DH}\\{CD=CD}\end{array}\right.$,
∴Rt△COD≌Rt△CHD,
∴CH=CO,
∴∠DBH=45°,∠DHB=90°,
∴BH=$\frac{\sqrt{2}}{2}$BD,
∴BC=CH+BH=CO+$\frac{\sqrt{2}}{2}$BD.
点评 此题考查全等三角形的判定与性质,等腰直角三角形的性质,利用等腰三角形的角度与边之间的关系是解决问题的关键.

 阅读快车系列答案
阅读快车系列答案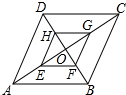 如图,在?ABCD中,对角线AC,BD相交于点O、E、F、G、H分别是OA、OB、OC、OD的中点.
如图,在?ABCD中,对角线AC,BD相交于点O、E、F、G、H分别是OA、OB、OC、OD的中点.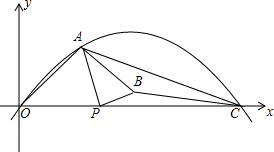 如图,抛物线y=ax2+bx+c经过点O(0,0),A(3,4)和C(11,0),点P(t,0)是x轴上的一个动点,以P为圆心,$\frac{1}{2}$AP长为半径,顺时针方向转90°得PB,连AB、BC、AC.
如图,抛物线y=ax2+bx+c经过点O(0,0),A(3,4)和C(11,0),点P(t,0)是x轴上的一个动点,以P为圆心,$\frac{1}{2}$AP长为半径,顺时针方向转90°得PB,连AB、BC、AC.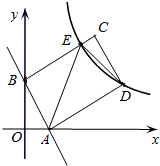 如图,矩形ABCD的顶点A、B分别在x轴、y轴上,AD=2AB,直线AB的解析式为y=-2x+4,双曲线y=$\frac{k}{x}$(x>0)经过点D,与BC边相交于点E.
如图,矩形ABCD的顶点A、B分别在x轴、y轴上,AD=2AB,直线AB的解析式为y=-2x+4,双曲线y=$\frac{k}{x}$(x>0)经过点D,与BC边相交于点E.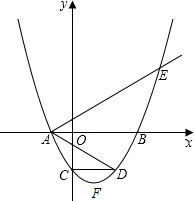 如图,二次函数y=a(x2-2mx-3m2)(其中a,m为常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B左侧),与y轴交于点C(0,-3),点D在二次函数图象上,且CD∥AB,连AD;过点A作射线AE交二次函数于点E,使AB平分∠DAE
如图,二次函数y=a(x2-2mx-3m2)(其中a,m为常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B左侧),与y轴交于点C(0,-3),点D在二次函数图象上,且CD∥AB,连AD;过点A作射线AE交二次函数于点E,使AB平分∠DAE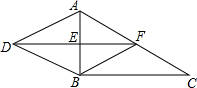 如图,在Rt△ABC中,∠ABC=90°,BC=2$\sqrt{3}$,E,F分别为AB,AC的中点,过点B作AC的平行线与FE的延长线交于点D,连接BF,AD.
如图,在Rt△ABC中,∠ABC=90°,BC=2$\sqrt{3}$,E,F分别为AB,AC的中点,过点B作AC的平行线与FE的延长线交于点D,连接BF,AD.