题目内容
11.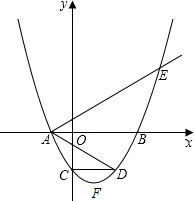 如图,二次函数y=a(x2-2mx-3m2)(其中a,m为常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B左侧),与y轴交于点C(0,-3),点D在二次函数图象上,且CD∥AB,连AD;过点A作射线AE交二次函数于点E,使AB平分∠DAE
如图,二次函数y=a(x2-2mx-3m2)(其中a,m为常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B左侧),与y轴交于点C(0,-3),点D在二次函数图象上,且CD∥AB,连AD;过点A作射线AE交二次函数于点E,使AB平分∠DAE(1)当a=1时,求点D的坐标;
(2)证明:无论a、m取何值,点E在同一直线上运动;
(3)设该二次函数图象顶点为F,试探究:在x轴上是否存在点P,使以PF、AD、AE为边构成的三角形是以AE为斜边的直角三角形?如果存在,请用含m的代数式表示点P的横坐标;如果不存在,请说明理由.
分析 (1)根据题意将a=1,C(0,-3)代入y=a(x2-2mx-3m2),进而求出m的值,即可得出答案;
(2)首先根据题意表示出A,B,C,D,进而联立$\left\{\begin{array}{l}{y=\frac{1}{m}x+1}\\{y=a({x}^{2}-2mx-3{m}^{2})}\end{array}\right.$,求出E点坐标即可得出答案;
(3)由(2)得:F(m,-4)、E(4m,5)、A(-m,0)、D(2m,-3),再利用PF,AD,AE的关系得出答案.
解答 解:(1)当a=1时,y=a(x2-2mx-3m2)=x2-2mx-3m2,
∵与y轴交于点C(0,-3),
∴-3m2=-3,
解得:m=±1,
∵m>0,
∴m=1,
∴抛物线解析式为:y=x2-2x-3=(x-1)2-4,
∵C,D关于直线x=1对称,
∴D点坐标为:(2,-3);
(2)作D关于AB对称的点D′必在AE上, 当y=0,则0=a(x2-2mx-3m2),
当y=0,则0=a(x2-2mx-3m2),
解得:x1=-m,x2=3m,
当x=0,y=-3am2,
可得:A(-m,0)、B(3m,0),C(0,-3am2),D(2m,-3am2)
∴D′(2m,3am2),
∵抛物线过点C,
∴-3am2=-3,
则am2=1,
∴直线AD′的解析式为:y=$\frac{1}{m}$x+1,
联立$\left\{\begin{array}{l}{y=\frac{1}{m}x+1}\\{y=a({x}^{2}-2mx-3{m}^{2})}\end{array}\right.$,整理得x2-3mx-4m2=0
解得x1=4m,x2=-m(舍去)
∴E(4m,5)
∴E在y=5上运动;
(3)由(2)得:F(m,-4)、E(4m,5)、A(-m,0)、D(2m,-3)
设P(b,0)
∴PF2=(m-b)2+16,AD2=9m2+9,AE2=25m2+25
∴(m-b)2+16+9m2+9=25m2+25,
解得:b1=-3m,b2=5m
∴P(-3m,0)或(5m,0).
点评 本题考查了二次函数性质、勾股定理及函数图象上点的坐标性质等知识,正确解方程得出解集进而得出E点坐标是解题关键.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案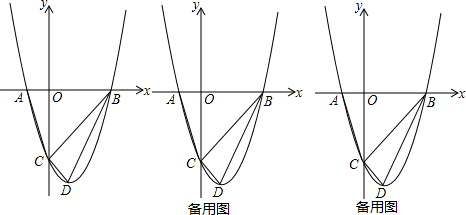
 如图所示的是一个三棱柱,用一个平面先后三次截这个三棱柱.
如图所示的是一个三棱柱,用一个平面先后三次截这个三棱柱.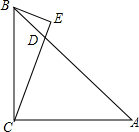 如图,等腰Rt△ABC中,∠ACB=90°,CA=CB,点D在AB上,AD=AC,BE⊥直线CD于E
如图,等腰Rt△ABC中,∠ACB=90°,CA=CB,点D在AB上,AD=AC,BE⊥直线CD于E 如图,若AE是△ABC边BC上的高,AD是∠EAC的角平分线交BC于D.若∠ACB=40°,则∠DAE等于25°.
如图,若AE是△ABC边BC上的高,AD是∠EAC的角平分线交BC于D.若∠ACB=40°,则∠DAE等于25°.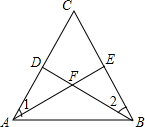 已知:如图,点D,E分别在△ABC的边AC和BC上,AE与BD相交于点F,给出下面四个条件:①∠1=∠2;②AD=BE;③AF=BF;④DF=EF,从这四个条件中选取两个,不能判定△ABC是等腰三角形的是( )
已知:如图,点D,E分别在△ABC的边AC和BC上,AE与BD相交于点F,给出下面四个条件:①∠1=∠2;②AD=BE;③AF=BF;④DF=EF,从这四个条件中选取两个,不能判定△ABC是等腰三角形的是( )