题目内容
8.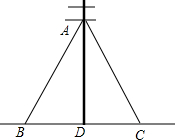 如图所示,为了固定电线杆AD,将两根长分别为10m的电线一端同系在电线杆A点上,另一端固定在地面上的两个锚上,那么两个锚(B,C)离电线杆底部(D)的距离相等吗?为什么?
如图所示,为了固定电线杆AD,将两根长分别为10m的电线一端同系在电线杆A点上,另一端固定在地面上的两个锚上,那么两个锚(B,C)离电线杆底部(D)的距离相等吗?为什么?
分析 利用全等三角形的判定定理HL得到Rt△ABD≌Rt△ACD,则该全等三角形的对应边相等:BD=CD.
解答 解:两个锚(B,C)离电线杆底部(D)的距离相等.理由如下:
依题意知,AD⊥BC,则∠ADB=∠ADC=90°.
在Rt△ABD与Rt△ACD中,$\left\{\begin{array}{l}{AD=AD}\\{AB=AC}\end{array}\right.$,
∴Rt△ABD≌Rt△ACD(HL),
∴BD=CD.
即两个锚(B,C)离电线杆底部(D)的距离相等.
点评 本题考查了全等三角形的应用,比较简单,关键在于利用全等三角形对应边相等判断BD=CD.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
18. 如图所示,P是⊙O的弦AB上的一点,AB=10cm,AP=4cm,OP=5cm,则⊙O的半径为( )cm.
如图所示,P是⊙O的弦AB上的一点,AB=10cm,AP=4cm,OP=5cm,则⊙O的半径为( )cm.
 如图所示,P是⊙O的弦AB上的一点,AB=10cm,AP=4cm,OP=5cm,则⊙O的半径为( )cm.
如图所示,P是⊙O的弦AB上的一点,AB=10cm,AP=4cm,OP=5cm,则⊙O的半径为( )cm.| A. | 5 | B. | 7 | C. | 6 | D. | 6.5 |
17.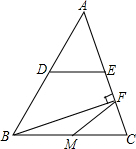 如图所示,△ABC中,BF为AC边上的高,点D、E、M分别为AB、AC、BC的中点.DE=6cm.则FM等于( )
如图所示,△ABC中,BF为AC边上的高,点D、E、M分别为AB、AC、BC的中点.DE=6cm.则FM等于( )
 如图所示,△ABC中,BF为AC边上的高,点D、E、M分别为AB、AC、BC的中点.DE=6cm.则FM等于( )
如图所示,△ABC中,BF为AC边上的高,点D、E、M分别为AB、AC、BC的中点.DE=6cm.则FM等于( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
 已知,如图,在四边形ABCD中,AB=AD,AB⊥BC,AD⊥DC.求证:DC=CB.
已知,如图,在四边形ABCD中,AB=AD,AB⊥BC,AD⊥DC.求证:DC=CB.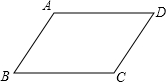 已知:如图,在四边形ABCD中,AB∥DC,AD∥BC,求证:AB=DC,AD=BC.
已知:如图,在四边形ABCD中,AB∥DC,AD∥BC,求证:AB=DC,AD=BC. 请用含字母的式子表示图形阴影部分的面积,并求阴影部分的面积.(结果保留π)
请用含字母的式子表示图形阴影部分的面积,并求阴影部分的面积.(结果保留π)