题目内容
1.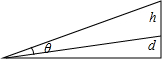 在一个艺术品陈列室内,一幅画的高度为h被悬挂于墙上,其底部边缘距离人的水平视线为d(如图),问人站在离墙多远欣赏这幅画最好?(换句话说怎样使得对应的θ最大)
在一个艺术品陈列室内,一幅画的高度为h被悬挂于墙上,其底部边缘距离人的水平视线为d(如图),问人站在离墙多远欣赏这幅画最好?(换句话说怎样使得对应的θ最大)
分析 设人里墙的距离为x,与画的上边缘仰角为α,与画的下边缘的仰角为β,可得tanα=$\frac{h+d}{x}$、tanβ=$\frac{d}{x}$,由tanθ=tan(α-β)=$\frac{tanα-tanβ}{1+tanαtanβ}$=$\frac{h}{x+\frac{d(h+d)}{x}}$知当x=$\frac{d(h+d)}{x}$,即x=$\sqrt{d(h+d)}$时,tanθ最大.
解答 解:如图,设人里墙的距离为x,与画的上边缘仰角为α,与画的下边缘的仰角为β,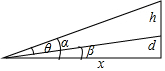
∵tanα=$\frac{h+d}{x}$,tanβ=$\frac{d}{x}$,
∴tanθ=tan(α-β)=$\frac{tanα-tanβ}{1+tanαtanβ}$=$\frac{\frac{h+d}{x}-\frac{d}{x}}{1+\frac{d(h+d)}{{x}^{2}}}$=$\frac{h}{x+\frac{d(h+d)}{x}}$,
当x=$\frac{d(h+d)}{x}$,即x=$\sqrt{d(h+d)}$时,tanθ最大,
答:人站在离墙$\sqrt{d(h+d)}$时欣赏这幅画最好.
点评 本题主要考查视角与三角函数的应用,用含x的表达式表示出tanθ是解题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
12.下列各组数中,相等的一组是( )
| A. | -(-2)3和-23 | B. | (-2)2和-22 | C. | -(-2)和-2 | D. | |-2|3和|2|3 |
13.若x为有理数,x-|x|表示的数是( )
| A. | 正数 | B. | 非正数 | C. | 负数 | D. | 非负数 |
11.多项式6πa3b2c2-x3y3z+m2n-110的次数是( )
| A. | 10次 | B. | 8次 | C. | 7次 | D. | 9次 |
 四点A、C、B、D顺次在一直线上,设AB=a,AC=b,AD=c,并且$\frac{1}{b}$+$\frac{1}{c}$=$\frac{2}{a}$,求证:$\frac{AC}{BC}$=$\frac{AD}{BD}$.
四点A、C、B、D顺次在一直线上,设AB=a,AC=b,AD=c,并且$\frac{1}{b}$+$\frac{1}{c}$=$\frac{2}{a}$,求证:$\frac{AC}{BC}$=$\frac{AD}{BD}$.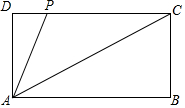 如图,在矩形ABCD中,AB=2,BC=1,P在DC上,当AP=$\frac{\sqrt{5}}{2}$时,△ADP∽△ABC.
如图,在矩形ABCD中,AB=2,BC=1,P在DC上,当AP=$\frac{\sqrt{5}}{2}$时,△ADP∽△ABC.