题目内容
16．
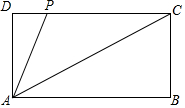如图，在矩形ABCD中，AB=2，BC=1，P在DC上，当AP=$\frac{\sqrt{5}}{2}$时，△ADP∽△ABC．
分析 根据矩形的性质和相似三角形的对应边成比例求得AP的长度．
解答 解：∵在矩形ABCD中，AB=2，BC=1，
∴AD=BC=1，AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{2}^{2}+{1}^{1}}$=$\sqrt{5}$．
由△ADP∽△ABC得到：$\frac{AD}{AB}$=$\frac{AP}{AC}$，即$\frac{1}{2}$=$\frac{AD}{\sqrt{5}}$，
解得AD=$\frac{\sqrt{5}}{2}$．
故答案是：$\frac{\sqrt{5}}{2}$．
点评 本题考查了矩形的性质和相似三角形的判定．解题时，要找准相似三角形的对应边．
练习册系列答案
阅读快车系列答案
相关题目
如图，△ABC是等边三角形，BD是中线，过点D作DE⊥AB于E交BC边延长线于F，AE=1．求BF的长．
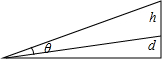在一个艺术品陈列室内，一幅画的高度为h被悬挂于墙上，其底部边缘距离人的水平视线为d（如图），问人站在离墙多远欣赏这幅画最好？（换句话说怎样使得对应的θ最大）