题目内容

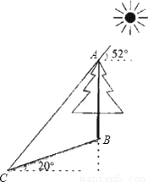
如图，在一个坡角为20°的斜坡上有一棵树，高为AB，当太阳光线与水平线成52°角时，测得该树斜坡上的树影BC的长为10m，求树高AB(精确到0.1m) (已知：sin20°≈0.342，cos20°≈0.940，tan20°≈0.364，sin52°≈0.788，cos52°≈0.616，tan52°≈1.280．供选用)

树高8.6米． 【解析】试题分析：过C作AB的垂线，设垂足为D．在Rt△CDB中，已知斜边BC=10m，利用三角函数求出CD和BD的长．同理在△ACD中，已知∠ACD=52°，CD，求出AD长，计算出AB=AD-BD，从而得到树的高度． 【解析】 作CD⊥AB于D． 在Rt△BCD中，BC=10m，∠BCD=20°， ∴CD=BC•cos20°≈10×0.940=9.40...
练习册系列答案
相关题目

如图，将三角尺的直角顶点放在直线a上，a∥b，∠1=50°，∠2=60°，求∠3的度数．

70°． 【解析】 试题分析：本题考查的是平行线的性质，三角形的内角和定理，掌握两直线平行，同位角相等是解决问题的前提．先根据三角形内角和定理求出∠4的度数，由对顶角相等求出∠5的度数，根据平行线的性质即可得出结论． 试题解析： 如图， ∵△BCD中，∠1=50°，∠2=60°， ∴∠4=180°﹣∠1﹣∠2=180°﹣50°﹣60°=70°， ∴∠5=∠...

五边形的内角和等于____度，十边形的对角线有__条.

540 35 【解析】【解析】 五边形的内角和=（5-2）×180°=540°，十边形的对角线条数=10×（10-3）÷2=35．故答案为：540；35．

用长为6m的铝合金型材做一个形状如图所示的矩形窗框，要使做成的窗框的透光面积最大，则该窗的长，宽应分别做成（　　）

A. 1.5m，1m B. 1m，0.5m C. 2m，1m D. 2m，0.5m

A 【解析】试题分析：设长为x，则宽为，S=，即S=， 要使做成的窗框的透光面积最大，则x=，于是宽为=1m， 所以要使做成的窗框的透光面积最大，则该窗的长，宽应分别做成1.5m，1m，故选A．

足球守门员大脚开出去的球的高度随时间的变化而变化，这一过程可近似地用下列哪幅图刻画（　　）

A. B. C. D.

B 【解析】【解析】 足球受力的作用后会升高，并向前运动，当足球动能减小后，足球不再升高，而逐渐下落，运动轨迹正好是一抛物线．故选B。

已知一个正六边形的边心距为，则它的半径为______ ．

2 【解析】试题分析：设正六边形的中心是O，一边是AB，过O作OG⊥AB与G，在直角△OAG中，根据三角函数即可求得OA． 【解析】 如图所示, 在Rt△AOG中,OG=,∠AOG=30°， ∴OA=OG÷cos 30°=÷=2； 故答案为：2.

如图，一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号，继续在同一深度直线航行4000米后，在B处测得俯角为60°的海底也有该黑匣子发出的信号，则黑匣子所在位置点C在海面下的深度为（ ）

A. 2000米 B. 4000米 C. 2000米 D. （2000+500）米

D 【解析】试题分析：由C点向AB作垂线，交AB的延长线于E点，并交海面于F点，易证∠BAC=∠BCA，所以有BA=BC．然后在直角△BCE中，利用正弦函数求出CE的长． 【解析】 由C点向AB作垂线，交AB的延长线于E点，并交海面于F点. 已知AB=4000(米),∠BAC=30°,∠EBC=60°， ∵∠BCA=∠EBC?∠BAC=30°， ∴∠BAC=∠BCA...

某工厂生产一种零件，计划在20天内完成，若每天多生产4个，则15天完成且还多生产10个．设原计划每天生产x个，根据题意可列方程为______．

20x＝15（x＋4）－10． 【解析】根据等量关系:实际15天完成的数量比计划20天完成的数量多10个,设原计划每天生产x个,原计划20天生产数量为:20x,实际15天生产的数量为:15(x+4),根据题意可列出方程为: 20x＝15（x＋4）－10,故答案为: 20x＝15（x＋4）－10.

如图，△ABC绕点C按顺时针旋转15°到△DEC，若点A恰好在DE上，则∠BAE的度数为（　　）

A. 15° B. 55° C. 65° D. 75°

A 【解析】试题解析：∵△ABC绕点C按顺时针旋转15°到△DEC， ∴∠ACD=15°，∠BAC=∠D， ∵∠EAC=∠D+∠ACD， 即∠BAE+∠BAC=∠D+∠ACD， ∴∠BAE=∠ACD=15°． 故选A．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网