题目内容
3.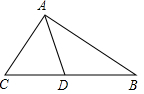 如图,△ABC中,∠C=2∠B,AD是△ABC的角平分线,求证:AB=AC+CD.
如图,△ABC中,∠C=2∠B,AD是△ABC的角平分线,求证:AB=AC+CD.
分析 首先在边AB上截取AP=AC,再证明△ACD≌△ADP,进而得到∠APD=∠B,PD=CD,再证明PD=PB即可.
解答 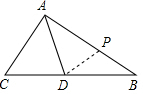 解:在AB上截取AP=AC,
解:在AB上截取AP=AC,
∵AD是△ABC的角平分线,
∴∠CAD=∠PAD,
在△ACD与△APD中,$\left\{\begin{array}{l}{AC=AP}\\{∠CAD=∠PAD}\\{AD=AD}\end{array}\right.$,
∴△ACD≌△APD,
∴CD=PD,∠C=∠APD,
∵∠C=2∠B,
∴∠APD=2∠B,
∵∠APD=∠B+∠BDP,
∴∠PDB=∠B,
∴PD=PB,
∴CD=PB,
∴AB=AP+PB=AC+CD.
点评 此题主要考查了全等三角形的判定与性质,关键是正确作出辅助线,掌握全等三角形的判定定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.今年“双11”,阿里仍选择在杭州西溪园区报告厅进行“天猫1111购物狂欢节”交易数据直播.“双11”活动结束,数据直播屏定格为:全天交易额571.12亿元,此数据用科学记数法可表示为( )
| A. | 5.7112×1012元 | B. | 5.7112×1011元 | C. | 5.7112×1010元 | D. | 5.7112×109元 |
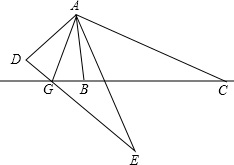 如图,△ABC外有E,D两点,DE=BC,EA=CA,∠ABC=∠ADE=90°,连接DE交CB的延长线于点G,连接AG,求证:GA平分∠DGB.
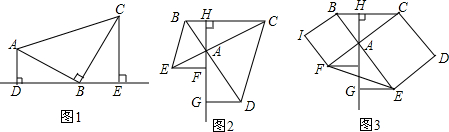
如图,△ABC外有E,D两点,DE=BC,EA=CA,∠ABC=∠ADE=90°,连接DE交CB的延长线于点G,连接AG,求证:GA平分∠DGB.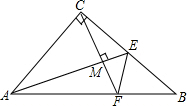 如图,△ABC中,AC=BC,∠ACB=90°.若AE为△ABC的中线,CF⊥AE,垂足为M,交AB于F点,求证:
如图,△ABC中,AC=BC,∠ACB=90°.若AE为△ABC的中线,CF⊥AE,垂足为M,交AB于F点,求证: