题目内容
12.先化简再求值:求(2m+n)(m-n)-(m+n)2-(4m2n2-8n4)÷(2n)2的值,其中m=$\frac{1}{2}$,n=-$\frac{5}{9}$.分析 首先利用多项式乘法法则以及完全平方公式计算,计算单项式的乘方,然后计算多项式与单项式的除法,然后合并同类项即可化简,最后代入数值计算即可.
解答 解:原式=(2m2+mn-2mn-n2)-(m2+n2+2mn)-(4m2n2-8n4)÷(4n2)
=2m2+mn-2mn-n2-m2-n2-2mn-(m2-2n2)
=2m2+mn-2mn-n2-m2-n2-2mn-m2+2n2
=-mn.
当m=$\frac{1}{2}$,n=-$\frac{5}{9}$时,原式=$\frac{1}{2}$×$\frac{5}{9}$=$\frac{5}{18}$.
点评 本题主要考查整式的混合运算,熟记公式正确确定运算顺序是解题的关键.

练习册系列答案
相关题目
20.下列说法正确的是( )
| A. | 直线AB和直线BA是两条直线 | B. | 射线AB和射线BA是两条射线 | ||
| C. | 线段AB和线段BA是两条线段 | D. | 直线和射线可以度量 |
17.$\sqrt{4}$的平方根等于( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±$\sqrt{2}$ |
2.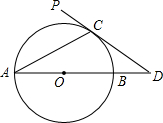 如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )
如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )
 如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )
如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )| A. | 2$\sqrt{2}$-2 | B. | 2-$\sqrt{2}$ | C. | 2$\sqrt{2}$-1 | D. | $\sqrt{2}$-1 |
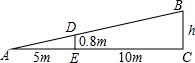 如图所示,小亮在打网球时,网高0.8m,网到拍的水平距离为10m,为使球恰好能打过网,而且落在离网5m位置上,求球拍击球的高度h.
如图所示,小亮在打网球时,网高0.8m,网到拍的水平距离为10m,为使球恰好能打过网,而且落在离网5m位置上,求球拍击球的高度h.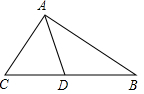 如图,△ABC中,∠C=2∠B,AD是△ABC的角平分线,求证:AB=AC+CD.
如图,△ABC中,∠C=2∠B,AD是△ABC的角平分线,求证:AB=AC+CD.