题目内容
先化简,再求值:(2cos60°+
)÷
,其中a=3.
| 3 |
| a-2 |
| a+tan45° |
| a2-4 |
考点:分式的化简求值,特殊角的三角函数值
专题:计算题
分析:先利用特殊角的三角函数值分别求出cos60°与tan45°的值,然后将括号中通分后,利用同分母分式的加法法则计算,同时将除式的分母利用平方差公式分解因式后,利用除以一个数等于乘以这个数的倒数把除法运算化为乘法运算,约分后得到最简结果,然后将a的值代入,即可求出原式的值.
解答:解:(2cos60°+
)÷
=(2×
+
)×
=(
+
)×
=
×
=a+2,
当a=3时,原式=3+2=5.
| 3 |
| a-2 |
| a+tan45° |
| a2-4 |
=(2×
| 1 |
| 2 |
| 3 |
| a-2 |
| (a+2)(a-2) |
| a+1 |
=(
| a-2 |
| a-2 |
| 3 |
| a-2 |
| (a+2)(a-2) |
| a+1 |
=
| a+1 |
| a-2 |
| (a+2)(a-2) |
| a+1 |
=a+2,
当a=3时,原式=3+2=5.
点评:此题考查了分式的化简求值,以及特殊角的三角函数值,分式的加减运算关键是通分,通分的关键是找出最简公分母;分式的乘除运算关键是约分,约分的关键是找出公因式,若出现多项式,应将多项式分解因式后再约分,同时注意将原式化简后再代值.

练习册系列答案
相关题目
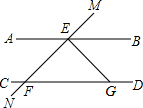 如图,两平行直线AB和CD被直线MN所截,交点分别为E、F,点G为射线FD上的一点,且EF=EG,若∠EFG=45°,则∠BEG为( )
如图,两平行直线AB和CD被直线MN所截,交点分别为E、F,点G为射线FD上的一点,且EF=EG,若∠EFG=45°,则∠BEG为( )| A、30° | B、45° |
| C、60° | D、90° |
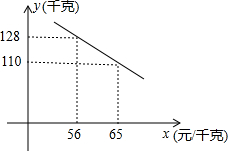 千克)与销售单价x(元/千克)关系如图所示,解答下列问题:
千克)与销售单价x(元/千克)关系如图所示,解答下列问题: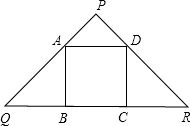 已知正方形ABCD内接于等腰直角三角形PQR,则PA:AQ=
已知正方形ABCD内接于等腰直角三角形PQR,则PA:AQ= 为了测量一个光盘的直径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出AB=6cm.这张光盘的直径是多少?
为了测量一个光盘的直径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出AB=6cm.这张光盘的直径是多少?