题目内容
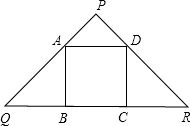 已知正方形ABCD内接于等腰直角三角形PQR,则PA:AQ=
已知正方形ABCD内接于等腰直角三角形PQR,则PA:AQ=考点:相似三角形的判定与性质,等腰直角三角形,正方形的性质
专题:
分析:由正方形ABCD内接于等腰直角三角形PQR,根据正方形与等腰三角形的性质,可得QB=BC=CR=AB,可得QR=3AB,又由AD∥BC,根据平行线分线段成比例定理,可求得
=
=
,继而求得PA:AQ的值.
| PA |
| PQ |
| AD |
| QR |
| 1 |
| 3 |
解答:解:∵四边形ABCD是正方形,
∴AD=AB=BC=CD,AD∥BC,∠ABC=90°,
∵△PQR是等腰直角三角形,
∴∠Q=45°,
∴QB=AB,
同理:CD=CR,
∴QR=BQ+BC+CR=3AB,
∵AD∥BC,
∴
=
=
,
∴PA:AQ=1:2.
故答案为:1:2.
∴AD=AB=BC=CD,AD∥BC,∠ABC=90°,
∵△PQR是等腰直角三角形,
∴∠Q=45°,
∴QB=AB,
同理:CD=CR,
∴QR=BQ+BC+CR=3AB,
∵AD∥BC,
∴
| PA |
| PQ |
| AD |
| QR |
| 1 |
| 3 |
∴PA:AQ=1:2.
故答案为:1:2.
点评:此题考查了正方形的性质、等腰直角三角形的性质以及平行线分线段成比例定理.此题难度不大,解题的关键是注意数形结合思想的应用,注意对应线段的对应关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知|a|=5,
=3,且ab<0,则a-b=( )
| b2 |
| A、8 | B、-2 |
| C、8或-8 | D、2或-2 |
已知分数a的分母是2012,分子是整数,为使|
-a|的数值最小,a的分子应当是( )
| 3 |
| 5 |
| A、1206 | B、1207 |
| C、1205 | D、1208 |
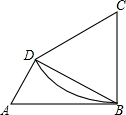 如图,有一四边形形状的铁皮ABCD,BC=CD=12,AB=2AD,∠ABC=∠ADB=90°,以C为圆心,CB为半径作弧BD得一扇形CBD,剪下扇形并用它围成一圆锥的侧面.则该圆锥的底面半径为
如图,有一四边形形状的铁皮ABCD,BC=CD=12,AB=2AD,∠ABC=∠ADB=90°,以C为圆心,CB为半径作弧BD得一扇形CBD,剪下扇形并用它围成一圆锥的侧面.则该圆锥的底面半径为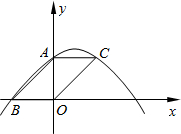 如图,?ABOC的顶点A、B、C在二次函数
如图,?ABOC的顶点A、B、C在二次函数