题目内容
11.已知(a-2)2+|b+1|=0,则代数式2a2b-3ab2-(a2b-4ab2)=-2.分析 根据条件可求出a与b的值,然后化简原式后,代入a与b的值即可求出答案.
解答 解:当a=2,b=-1时,
原式=2a2b-3ab2-a2b+4ab2
=a2b+ab2
=4×(-1)+2×1
=-4+2
=-2
故答案为:-2
点评 本题考查整式的运算,解题的关键是熟练运用整式的运算法则,本题属于基础题型.

练习册系列答案
相关题目
19.【问题提出】
我们借助学习“图形的判定”获得的经验与方法对“平行四边形的判定”进一步探究.
【初步思考】
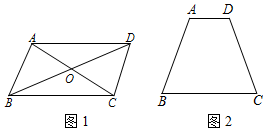
在一个四边形中,我们把“一组对边平行、一组对边相等、一组对角相等或一条对角线被另一条对角线平分”称为一个条件.如图1,四边形ABCD中,我们用符号语言表示出所有的8个条件:
那么满足2个条件的四边形是不是平行四边形呢?
【深入探究】
小莉所在学习小组进行了研究,她们认为2个条件可分为以下六种类型:
Ⅰ关于对边的2个条件;Ⅱ关于对角的2个条件;
Ⅲ关于对角线的2个条件;Ⅳ关于边的条件与角的条件各1个;
Ⅴ关于边的条件与对角线的条件各1个;Ⅵ关于角的条件与对角线的条件各1个.
(1)小明认为“Ⅰ关于对边的2个条件”可分为“①②,③④,①③,①④”共4种不同种类的情形.请你仿照小明的叙述对其它五种类型进一步分类.
(2)小红认为有4种情形是平行四边形的判定依据.请你写出其它的三个判定定理.
定义:两组对边分别平行的四边形是平行四边形;
定理1:两组对边分别相等的四边形是平行四边形;
定理2:一组对边平行且相等的四边形是平行四边形;
定理3:对角线互相平分的四边形是平行四边形.
(3)小刚认为除了4个判定依据外,还存在一些真命题,他写出了其中的1个,请证明这个真命题,并仿照他的格式写出其它真命题(无需证明):
真命题1:四边形ABCD中,若∠BAD=∠BCD,∠ABC=∠ADC,则四边形ABCD是平行四边形.
(4)小亮认为,还存在一些假命题,他写出了其中的1个,并举反例进行了说明,请你仿照小亮的格式写出其它假命题并举反例进行说明.
假命题1:四边形ABCD中,若AB=CD,AD∥BC,则四边形ABCD不一定是平行四边形.
反例说明:如图2,四边形ABCD中,AB=CD,AD∥BC,显然四边形ABCD不是平行四边形.
我们借助学习“图形的判定”获得的经验与方法对“平行四边形的判定”进一步探究.

【初步思考】
在一个四边形中,我们把“一组对边平行、一组对边相等、一组对角相等或一条对角线被另一条对角线平分”称为一个条件.如图1,四边形ABCD中,我们用符号语言表示出所有的8个条件:
| ①AB=CD; | ②AD=BC; | ③AB∥CD; | ④AD∥BC; |
| ⑤∠BAD=∠BCD; | ⑥∠ABC=∠ADC; | ⑦OA=OC; | ⑧OB=OD. |
【深入探究】
小莉所在学习小组进行了研究,她们认为2个条件可分为以下六种类型:
Ⅰ关于对边的2个条件;Ⅱ关于对角的2个条件;
Ⅲ关于对角线的2个条件;Ⅳ关于边的条件与角的条件各1个;
Ⅴ关于边的条件与对角线的条件各1个;Ⅵ关于角的条件与对角线的条件各1个.
(1)小明认为“Ⅰ关于对边的2个条件”可分为“①②,③④,①③,①④”共4种不同种类的情形.请你仿照小明的叙述对其它五种类型进一步分类.
(2)小红认为有4种情形是平行四边形的判定依据.请你写出其它的三个判定定理.
定义:两组对边分别平行的四边形是平行四边形;
定理1:两组对边分别相等的四边形是平行四边形;
定理2:一组对边平行且相等的四边形是平行四边形;
定理3:对角线互相平分的四边形是平行四边形.
(3)小刚认为除了4个判定依据外,还存在一些真命题,他写出了其中的1个,请证明这个真命题,并仿照他的格式写出其它真命题(无需证明):
真命题1:四边形ABCD中,若∠BAD=∠BCD,∠ABC=∠ADC,则四边形ABCD是平行四边形.
(4)小亮认为,还存在一些假命题,他写出了其中的1个,并举反例进行了说明,请你仿照小亮的格式写出其它假命题并举反例进行说明.
假命题1:四边形ABCD中,若AB=CD,AD∥BC,则四边形ABCD不一定是平行四边形.
反例说明:如图2,四边形ABCD中,AB=CD,AD∥BC,显然四边形ABCD不是平行四边形.
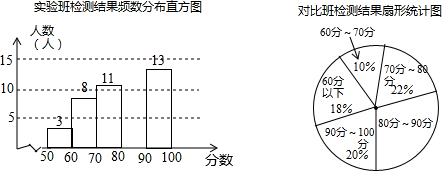
1.“弘扬雷锋精神,共建幸福沈阳”,幸福沈阳需要830万沈阳人共同缔造,将数据830万用科学记数法可以表示为( )万.
| A. | 83×10 | B. | 8.3×102 | C. | 8.3×103 | D. | 0.83×103 |
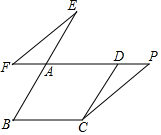 如图,在平行四边形ABCD中,延长BA至点E,使AE=AB,点F、P在边AD所在的直线上,EF∥CP.
如图,在平行四边形ABCD中,延长BA至点E,使AE=AB,点F、P在边AD所在的直线上,EF∥CP.