题目内容
6.若m+$\sqrt{{m}^{2}}$=2m,则m的取值范围是m≥0.分析 根据二次根式的性质,可得答案.
解答 解:由m+$\sqrt{{m}^{2}}$=2m,得
m+m=2m,即m≥0,
故答案为:m≥0.
点评 本题考查了二次根式的性质与化简,利用二次根式的性质$\sqrt{{a}^{2}}$=a (a≥0)是解题关键.

练习册系列答案
相关题目
17.科书补助的部分情况:
求获得免费提供教科书补助的七年级的学生人数.
| 年级 项目 | 七 | 八 | 九 | 合计 |
| 每人免费补助金额/元 | 109 | 94 | 47.5 | |
| 人数/人 | 40 | 120 | ||
| 免费补助金额/元 | 1900 | 10095 |
14.若方程(2a+1)x2+bx+c=0是关于x的一元一次方程,则字母系数a,b,c的值必须满足( )
| A. | a=-$\frac{1}{2}$,b≠0,c为任何数 | B. | a≠$\frac{1}{2}$,b≠0,c=0 | ||
| C. | a=-$\frac{1}{2}$,b≠0,c≠0 | D. | a=$\frac{1}{2}$,b=0,c为任何数 |
3.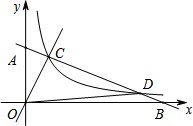 如图,在平面直角坐标系中,直线AB与双曲线$y=\frac{2}{x}$相交于C、D两点,已知直线OC解析式为y=2x,S△AOD=6,则D点的坐标为( )
如图,在平面直角坐标系中,直线AB与双曲线$y=\frac{2}{x}$相交于C、D两点,已知直线OC解析式为y=2x,S△AOD=6,则D点的坐标为( )
 如图,在平面直角坐标系中,直线AB与双曲线$y=\frac{2}{x}$相交于C、D两点,已知直线OC解析式为y=2x,S△AOD=6,则D点的坐标为( )
如图,在平面直角坐标系中,直线AB与双曲线$y=\frac{2}{x}$相交于C、D两点,已知直线OC解析式为y=2x,S△AOD=6,则D点的坐标为( )| A. | $(3,\frac{2}{3})$ | B. | $(4,\frac{1}{2})$ | C. | $(5,\frac{2}{5})$ | D. | $(6,\frac{1}{3})$ |
10.已知反比例函数y=-$\frac{1}{x}$,下列结论正确的是( )
| A. | y的值随着x的增大而减小 | |
| B. | 图象是双曲线,是中心对称图形且是轴对称 | |
| C. | 当x>1时,0<y<1 | |
| D. | 图象可能与坐标轴相交 |
7.一个钝角三角形的两边长为5、12,则第三边可以为( )
| A. | 11 | B. | 13 | C. | 15 | D. | 17 |
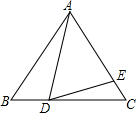 如图,在边长为18的正三角形ABC中,BD=6,∠ADE=60°,则AE的长为14.
如图,在边长为18的正三角形ABC中,BD=6,∠ADE=60°,则AE的长为14.