题目内容
3.三个同学对问题“若方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$,求方程组$\left\{\begin{array}{l}{3{a}_{1}x+2{b}_{1}y=5{c}_{1}}\\{3{a}_{2}x+2{b}_{2}y=5{c}_{2}}\end{array}\right.$的解.”提出各自的想法. 甲说:“这个题目好象条件不够,不能求解”; 乙说:“它们的系数有一定的规律,可以试试”; 丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替代的方法来解决”.参考他们的讨论,你认为这个题目的解应该是( )| A. | $\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=3\\ y=4\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=5\\ y=10\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=6\\ y=8\end{array}\right.$ |
分析 把第二个方程组的两个方程的两边都除以5,通过换元替代的方法即可得到一个关于x,y的方程组,即可求解.
解答 解:第二个方程组的两个方程的两边都除以5得:$\left\{\begin{array}{l}{\frac{3}{5}{a}_{1}x+\frac{2}{5}{b}_{1}y={c}_{1}}\\{\frac{3}{5}{a}_{2}x+\frac{2}{5}{b}_{2}y={c}_{2}}\end{array}\right.$,
∵方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$,
∴$\left\{\begin{array}{l}{\frac{3}{5}x=3}\\{\frac{2}{5}y=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=5}\\{y=10}\end{array}\right.$.
故选C.
点评 本题主要考查了方程组的解法,正确观察已知方程的系数之间的关系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知点A(a,1)与点B(5,b)关于点(3,2)对称,则a+b=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
8.据调查,2011年5月茶陵县的房价均价为2600元/m2,2013年同期将达到3200元/m2,假设这两年茶陵县房价的平均增长率为x,根据题意,所列方程为( )
| A. | 2600(1+x%)2=3200 | B. | 2600(1-x%)2=3200 | C. | 2600(1+x)2=3200 | D. | 2600(1+x)2=3200 |
12.已知二元一次方程x+y=1,下列说法不正确的是( )
| A. | 它有无数多组解 | B. | 它只有一组非负整数解 | ||
| C. | 它有无数多组整数解 | D. | 它没有正整数解 |

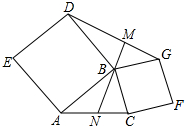 若以△ABC的边AB,BC为边向三角形外作正方形ABDE,BCFG,N为AC中点,求证:DG=2BN,BM⊥DG.
若以△ABC的边AB,BC为边向三角形外作正方形ABDE,BCFG,N为AC中点,求证:DG=2BN,BM⊥DG.