题目内容
6.若关于x的方程a(x+m)2+b=0的解是x1=-3,x2=1(a、m、b均为常数,a≠0),则方程a(x+2+m)2+b=0的解是-5或-1.分析 根据题意得出x与a,b,m的关系进而,将方程a(x+m+3)2=b变形求出解即可.
解答 解:方法一:∵方程a(x+m)2=b的两根分别为x1=-3,x2=1(a,b,m为常数),
∴(x+m)2=$\frac{b}{a}$,
∴x+m=±$\sqrt{\frac{b}{a}}$,
∴-m±$\sqrt{\frac{b}{a}}$=-3或1,
∴a(x+m+3)2=b可变形为:
x+m+2=±$\sqrt{\frac{b}{a}}$,
∴x=-m±$\sqrt{\frac{b}{a}}$-2
∴方程a(x+m+2)2=b的两根是:-3-2=-5或1-2=-1.
故答案为:-5或-1.
方法二:由题意可知二次函数y=a(x十m)2+b与x轴的交点为(一3,0)和(1,0),
将函数向左平移2个单位,则交点为(一5,0)和(一1,0),所以方程的根为一5和一1.
点评 此题考查了解一元二次方程-直接开平方法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
14.关于x的一元二次方程x2+k=0有实数根,则( )
| A. | k<0 | B. | k>0 | C. | k≥0 | D. | k≤0 |
1.若二次函数y=(m+1)x2-mx+m2-2m-3的图象经过原点,则m的值必为( )
| A. | -1或3 | B. | -1 | C. | 3 | D. | -3或1 |
11.关于x的一元二次方程x2-ax=5的一个根是-1,则a的值是(( )
| A. | -1 | B. | 1 | C. | 4 | D. | -4 |
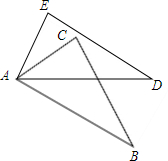 如图所示,AB=AD,AC=AE,BC=DE,如果∠EAD=70°,∠CAD=40°,求∠BAD的度数.
如图所示,AB=AD,AC=AE,BC=DE,如果∠EAD=70°,∠CAD=40°,求∠BAD的度数.