题目内容
2.已知,关于x的方程x2-2mx+m2-1=0.(1)不解方程,判断此方程根的情况;
(2)若x=2是该方程的一个根,求代数式-2m2+8m-3的值.
分析 (1)根据方程的系数结合根的判别式即可得出△=4>0,由此得出方程有两个不相等的实数根;
(2)将x=2代入原方程可求出m2-4m=-3,将其代入代数式-2m2+8m-3中即可得出结论.
解答 解:(1)∵在方程x2-2mx+m2-1=0中,△=(-2m)2-4×1×(m2-1)=4>0,
∴方程x2-2mx+m2-1=0有两个不相等的实数根.
(2)将x=2代入原方程中,得:4-4m+m2-1=0,
即m2-4m=-3,
∴-2m2+8m-3=-2(m2-4m)-3=3.
点评 本题考查了根的判别式以及一元二次方程的解,熟练掌握“当根的判别式△>0时方程有两个不相等的实数根.”是解题的关键.

练习册系列答案
相关题目
10.(1)根据图示规律填表:

(2)猜想:第n个图形共有多少个正方形?

| 图形编号 | 1×1的正方形个数 | 2×2的正方形个数 | 3×3的正方形个数 | 4×4的正方形个数 |
| ① | ||||
| ② | ||||
| ③ | ||||
| ④ |
7.方程x2=9的解是( )
| A. | x=3 | B. | x=-3 | C. | x=±3 | D. | x=±$\sqrt{3}$ |
12.抛物线y=x2-1与y轴的交点坐标是( )
| A. | (0,1) | B. | (0,-1) | C. | (1,0) | D. | (-1,0) |
 如图,已知抛物线与x轴交于A(-1,0)、B(5,0)两点,与y轴交于点C(0,5).
如图,已知抛物线与x轴交于A(-1,0)、B(5,0)两点,与y轴交于点C(0,5).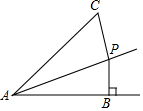 如图,点P是∠BAC的平分线上一点,PB⊥AB于B,且PB=5,AC=12,则△APC的面积是30.
如图,点P是∠BAC的平分线上一点,PB⊥AB于B,且PB=5,AC=12,则△APC的面积是30.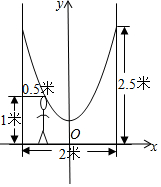 如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子.
如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子.